mirror of
https://github.com/rsheldiii/KeyV2.git
synced 2025-09-14 16:19:50 +00:00
add a massive chunk of stuff because you forgot to keep doing atomic commits
This commit is contained in:
parent
f252ec2c30
commit
6d2bb24ccb
31 changed files with 668 additions and 674 deletions
116
src/dishes.scad
Normal file
116
src/dishes.scad
Normal file
|
|
@ -0,0 +1,116 @@
|
|||
include <libraries/geodesic_sphere.scad>
|
||||
include <shapes.scad>
|
||||
//geodesic looks much better, but runs very slow for anything above a 2u
|
||||
geodesic=false;
|
||||
|
||||
//dish selector
|
||||
module dish(width, height, depth, inverted, tilt) {
|
||||
if($dish_type == "cylindrical"){
|
||||
cylindrical_dish(width, height, depth, inverted, tilt);
|
||||
}
|
||||
else if ($dish_type == "spherical") {
|
||||
spherical_dish(width, height, depth, inverted, tilt);
|
||||
}
|
||||
else if ($dish_type == "sideways cylindrical"){
|
||||
sideways_cylindrical_dish(width, height, depth, inverted, tilt);
|
||||
}
|
||||
else if ($dish_type == "old spherical") {
|
||||
old_spherical_dish(width, height, depth, inverted, tilt);
|
||||
}
|
||||
// else no dish, "no dish" is the value
|
||||
}
|
||||
|
||||
module cylindrical_dish(width, height, depth, inverted, tilt){
|
||||
// .5 has problems starting around 3u
|
||||
$fa=.25;
|
||||
/* we do some funky math here
|
||||
* basically you want to have the dish "dig in" to the keycap x millimeters
|
||||
* in order to do that you have to solve a small (2d) system of equations
|
||||
* where the chord of the spherical cross section of the dish is
|
||||
* the width of the keycap.
|
||||
*/
|
||||
// the distance you have to move the dish so it digs in depth millimeters
|
||||
chord_length = (pow(width, 2) - 4 * pow(depth, 2)) / (8 * depth);
|
||||
//the radius of the dish
|
||||
rad = (pow(width, 2) + 4 * pow(depth, 2)) / (8 * depth);
|
||||
direction = inverted ? -1 : 1;
|
||||
|
||||
rotate([90-tilt,0,0]){
|
||||
translate([0,chord_length * direction,0]){
|
||||
cylinder(h=height + 20, r=rad, center=true);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module sideways_cylindrical_dish(width, height, depth, inverted, tilt){
|
||||
$fa=1;
|
||||
chord_length = (pow(height, 2) - 4 * pow(depth, 2)) / (8 * depth);
|
||||
rad = (pow(height, 2) + 4 * pow(depth, 2)) / (8 * depth);
|
||||
|
||||
direction = inverted ? -1 : 1;
|
||||
|
||||
rotate([90,tilt,90]){
|
||||
translate([0,chord_length * direction,0]){
|
||||
cylinder(h = width + 20,r=rad, center=true); // +20 for fudge factor
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module spherical_dish(width, height, depth, inverted, tilt, txt=""){
|
||||
|
||||
//same thing as the cylindrical dish here, but we need the corners to just touch - so we have to find the hypotenuse of the top
|
||||
chord = pow((pow(width,2) + pow(height, 2)),0.5); //getting diagonal of the top
|
||||
|
||||
// the distance you have to move the dish up so it digs in depth millimeters
|
||||
chord_length = (pow(chord, 2) - 4 * pow(depth, 2)) / (8 * depth);
|
||||
//the radius of the dish
|
||||
rad = (pow(chord, 2) + 4 * pow(depth, 2)) / (8 * depth);
|
||||
direction = inverted ? -1 : 1;
|
||||
|
||||
/*intersection(){*/
|
||||
rotate([-tilt,0,0]){
|
||||
translate([0,0,0 * direction]){
|
||||
if (geodesic){
|
||||
$fa=20;
|
||||
scale([chord/2/depth, chord/2/depth]) {
|
||||
geodesic_sphere(r=depth);
|
||||
}
|
||||
} else {
|
||||
$fa=7;
|
||||
// rotate 1 because the bottom of the sphere looks like trash.
|
||||
scale([chord/2/depth, chord/2/depth]) {
|
||||
geodesic_sphere(r=depth);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
//the older, 'more accurate', and MUCH slower spherical dish.
|
||||
// generates the largest sphere possible that still contains the chord we are looking for
|
||||
// much more graduated curvature at an immense cost
|
||||
module old_spherical_dish(width, height, depth, inverted, tilt, txt=""){
|
||||
|
||||
//same thing as the cylindrical dish here, but we need the corners to just touch - so we have to find the hypotenuse of the top
|
||||
chord = pow((pow(width,2) + pow(height, 2)),0.5); //getting diagonal of the top
|
||||
|
||||
// the distance you have to move the dish up so it digs in depth millimeters
|
||||
chord_length = (pow(chord, 2) - 4 * pow(depth, 2)) / (8 * depth);
|
||||
//the radius of the dish
|
||||
rad = (pow(chord, 2) + 4 * pow(depth, 2)) / (8 * depth);
|
||||
direction = inverted ? -1 : 1;
|
||||
|
||||
/*intersection(){*/
|
||||
rotate([-tilt,0,0]){
|
||||
translate([0,0,chord_length * direction]){
|
||||
if (geodesic){
|
||||
$fa=7;
|
||||
geodesic_sphere(r=rad);
|
||||
} else {
|
||||
$fa=1;
|
||||
// rotate 1 because the bottom of the sphere looks like trash
|
||||
sphere(r=rad);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
250
src/key.scad
Normal file
250
src/key.scad
Normal file
|
|
@ -0,0 +1,250 @@
|
|||
// files
|
||||
include <shapes.scad>
|
||||
include <stems.scad>
|
||||
include <dishes.scad>
|
||||
include <libraries/geodesic_sphere.scad>
|
||||
|
||||
/* [Fancy Bowed Sides] */
|
||||
|
||||
|
||||
// if you're doing fancy bowed keycap sides, this controls how many slices you take
|
||||
// default of 1 for no sampling, just top/bottom
|
||||
height_slices = 1;
|
||||
enable_side_sculpting = false;
|
||||
|
||||
|
||||
|
||||
|
||||
/* [Hidden] */
|
||||
$fs = .1;
|
||||
//beginning to use unit instead of baked in 19.05
|
||||
unit = 19.05;
|
||||
//minkowski radius. radius of sphere used in minkowski sum for minkowski_key function. 1.75 default for faux G20
|
||||
$minkowski_radius = .33;
|
||||
|
||||
|
||||
|
||||
|
||||
// derived values. can't be variables if we want them to change when the special variables do
|
||||
|
||||
// actual mm key width and height
|
||||
function total_key_width() = $bottom_key_width + unit * ($key_length - 1);
|
||||
function total_key_height() = $bottom_key_height + unit * ($key_height - 1);
|
||||
|
||||
// actual mm key width and height at the top
|
||||
function top_total_key_width() = $bottom_key_width + (unit * ($key_length - 1)) - $width_difference;
|
||||
function top_total_key_height() = $bottom_key_height + (unit * ($key_height - 1)) - $height_difference;
|
||||
|
||||
// side sculpting functions
|
||||
// bows the sides out on stuff like SA and DSA keycaps
|
||||
function side_sculpting(progress) = (1 - progress) * 2.5;
|
||||
// makes the rounded corners of the keycap grow larger as they move upwards
|
||||
function corner_sculpting(progress) = pow(progress, 2);
|
||||
|
||||
|
||||
// key shape including dish. used as the ouside and inside shape in key()
|
||||
module shape(thickness_difference, depth_difference){
|
||||
intersection(){
|
||||
dished(depth_difference, $inverted_dish) {
|
||||
color([.2667,.5882,1]) shape_hull(thickness_difference, depth_difference);
|
||||
}
|
||||
if ($inverted_dish) {
|
||||
// larger shape_hull to clip off bits of the inverted dish
|
||||
color([.5412, .4784, 1]) shape_hull(thickness_difference, 0, 2);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// shape of the key but with soft, rounded edges. much more realistic, MUCH more complex. orders of magnitude more complex
|
||||
module rounded_shape() {
|
||||
render(){
|
||||
minkowski(){
|
||||
// half minkowski. that means the shape is neither circumscribed nor inscribed.
|
||||
shape($minkowski_radius * 2, $minkowski_radius/2);
|
||||
difference(){
|
||||
sphere(r=$minkowski_radius, $fn=24);
|
||||
translate([0,0,-$minkowski_radius])
|
||||
cube([2*$minkowski_radius,2*$minkowski_radius,2*$minkowski_radius], center=true);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// basic key shape, no dish, no inside
|
||||
// which is only used for dishing to cut the dish off correctly
|
||||
// $height_difference used for keytop thickness
|
||||
// extra_slices is a hack to make inverted dishes still work
|
||||
module shape_hull(thickness_difference, depth_difference, extra_slices = 0){
|
||||
render() {
|
||||
if ($linear_extrude_shape) {
|
||||
linear_extrude_shape_hull(thickness_difference, depth_difference, extra_slices);
|
||||
} else {
|
||||
hull_shape_hull(thickness_difference, depth_difference, extra_slices);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
//corollary is shape_hull
|
||||
// extra_slices unused, only to match argument signatures
|
||||
module linear_extrude_shape_hull(thickness_difference, depth_difference, extra_slices = 0){
|
||||
|
||||
height = $total_depth - depth_difference;
|
||||
width_scale = top_total_key_width() / total_key_width();
|
||||
height_scale = top_total_key_height() / total_key_height();
|
||||
|
||||
translate([0,$linear_extrude_height_adjustment,0]){
|
||||
linear_extrude(height = height, scale = [width_scale, height_scale]) {
|
||||
translate([0,-$linear_extrude_height_adjustment,0]){
|
||||
key_shape(total_key_width(), total_key_height(), thickness_difference, thickness_difference, $corner_radius);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module hull_shape_hull(thickness_difference, depth_difference, extra_slices = 0) {
|
||||
slices = 10;
|
||||
for (index = [0:$height_slices - 1 + extra_slices]) {
|
||||
hull() {
|
||||
shape_slice(index / $height_slices, thickness_difference, depth_difference);
|
||||
shape_slice((index + 1) / $height_slices, thickness_difference, depth_difference);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module shape_slice(progress, thickness_difference, depth_difference) {
|
||||
// makes the sides bow
|
||||
extra_side_size = $enable_side_sculpting ? side_sculpting(progress) : 0;
|
||||
// makes the rounded corners of the keycap grow larger as they move upwards
|
||||
extra_corner_size = $enable_side_sculpting ? corner_sculpting(progress) : 0;
|
||||
|
||||
// computed values for this slice
|
||||
extra_width_this_slice = ($width_difference - extra_side_size) * progress;
|
||||
extra_height_this_slice = ($height_difference - extra_side_size) * progress;
|
||||
skew_this_slice = $top_skew * progress;
|
||||
depth_this_slice = ($total_depth - depth_difference) * progress;
|
||||
tilt_this_slice = -$top_tilt / $key_height * progress;
|
||||
|
||||
translate([0, skew_this_slice, depth_this_slice]) {
|
||||
rotate([tilt_this_slice,0,0]){
|
||||
linear_extrude(height = 0.001){
|
||||
key_shape(
|
||||
total_key_width(),
|
||||
total_key_height(),
|
||||
thickness_difference+extra_width_this_slice,
|
||||
thickness_difference+extra_height_this_slice,
|
||||
$corner_radius + extra_corner_size
|
||||
);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module dished(depth_difference, inverted = false) {
|
||||
if (inverted) {
|
||||
union() {
|
||||
children();
|
||||
translate([$dish_skew_x, $top_skew + $dish_skew_y, $total_depth - depth_difference]){
|
||||
color([.4078, .3569, .749]) dish(top_total_key_width() + $dish_overdraw_width, top_total_key_height() + $dish_overdraw_height, $dish_depth, $inverted_dish, $top_tilt / $key_height);
|
||||
}
|
||||
}
|
||||
} else {
|
||||
difference() {
|
||||
children();
|
||||
translate([$dish_skew_x, $top_skew + $dish_skew_y, $total_depth - depth_difference]){
|
||||
color([.4078, .3569, .749]) dish(top_total_key_width() + $dish_overdraw_width, top_total_key_height() + $dish_overdraw_height, $dish_depth, $inverted_dish, $top_tilt / $key_height);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// puts it's children at the center of the dishing on the key. this DOES rotate them though, it's not straight up
|
||||
module top_of_key(){
|
||||
extra_dish_depth = ($dish_type == "no dish") ? 0 : $dish_depth;
|
||||
translate([$dish_skew_x, $top_skew + $dish_skew_y, $total_depth - extra_dish_depth]){
|
||||
rotate([-$top_tilt,0,0]){
|
||||
children();
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module keytext() {
|
||||
extra_inset_depth = ($inset_text) ? 0.3 : 0;
|
||||
|
||||
translate([0, 0, -extra_inset_depth]){
|
||||
top_of_key(){
|
||||
linear_extrude(height=$dish_depth){
|
||||
text(text=$text, font=$font, size=$font_size, halign="center", valign="center");
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module connectors() {
|
||||
intersection() {
|
||||
for (connector_pos = $connectors) {
|
||||
translate([connector_pos[0], connector_pos[1], $stem_inset]) {
|
||||
rotate([0, 0, $stem_rotation]){
|
||||
color([1, .6941, .2]) connector($stem_profile, $total_depth, $has_brim, $slop, $stem_inset, $support_type);
|
||||
}
|
||||
}
|
||||
}
|
||||
// cut off anything that isn't underneath the keytop
|
||||
shape($wall_thickness, $keytop_thickness);
|
||||
}
|
||||
}
|
||||
|
||||
//approximate (fully depressed) cherry key to check clearances
|
||||
module clearance_check() {
|
||||
if($clearance_check == true && ($stem_profile == "cherry" || $stem_profile == "cherry_rounded")){
|
||||
color([1,0,0, 0.5]){
|
||||
translate([0,0,3.6 + $stem_inset - 5]) {
|
||||
%hull() {
|
||||
cube([15.6, 15.6, 0.01], center=true);
|
||||
translate([0,1,5 - 0.01]) cube([10.5,9.5, 0.01], center=true);
|
||||
}
|
||||
%hull() {
|
||||
cube([15.6, 15.6, 0.01], center=true);
|
||||
translate([0,0,-5.5]) cube([13.5,13.5,0.01], center=true);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module keytop() {
|
||||
difference(){
|
||||
if ($rounded_key) {
|
||||
rounded_shape();
|
||||
} else {
|
||||
shape(0, 0);
|
||||
}
|
||||
translate([0,0,-0.01]) shape($wall_thickness, $keytop_thickness);
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
// The final, penultimate key generation function.
|
||||
// takes all the bits and glues them together. requires configuration with special variables.
|
||||
module key() {
|
||||
difference() {
|
||||
union(){
|
||||
keytop();
|
||||
if($stem_profile != "blank") connectors();
|
||||
if(!$inset_text) keytext();
|
||||
clearance_check();
|
||||
top_of_key() {
|
||||
children();
|
||||
}
|
||||
}
|
||||
if ($inset_text) keytext();
|
||||
}
|
||||
}
|
||||
|
||||
// actual full key with space carved out and keystem/stabilizer connectors
|
||||
// this is an example key with all the fixins
|
||||
module example_key(){
|
||||
include <settings.scad>
|
||||
key();
|
||||
}
|
||||
|
||||
example_key();
|
||||
110
src/libraries/geodesic_sphere.scad
Normal file
110
src/libraries/geodesic_sphere.scad
Normal file
|
|
@ -0,0 +1,110 @@
|
|||
// from https://www.thingiverse.com/thing:1484333
|
||||
// public domain license
|
||||
// same syntax and semantics as built-in sphere, so should be a drop-in replacement
|
||||
// it's a bit slow for large numbers of facets
|
||||
module geodesic_sphere(r=-1, d=-1) {
|
||||
// if neither parameter specified, radius is taken to be 1
|
||||
rad = r > 0 ? r : d > 0 ? d/2 : 1;
|
||||
|
||||
pentside_pr = 2*sin(36); // side length compared to radius of a pentagon
|
||||
pentheight_pr = sqrt(pentside_pr*pentside_pr - 1);
|
||||
// from center of sphere, icosahedron edge subtends this angle
|
||||
edge_subtend = 2*atan(pentheight_pr);
|
||||
|
||||
// vertical rotation by 72 degrees
|
||||
c72 = cos(72);
|
||||
s72 = sin(72);
|
||||
function zrot(pt) = [ c72*pt[0]-s72*pt[1], s72*pt[0]+c72*pt[1], pt[2] ];
|
||||
|
||||
// rotation from north to vertex along positive x
|
||||
ces = cos(edge_subtend);
|
||||
ses = sin(edge_subtend);
|
||||
function yrot(pt) = [ ces*pt[0] + ses*pt[2], pt[1], ces*pt[2]-ses*pt[0] ];
|
||||
|
||||
// 12 icosahedron vertices generated from north, south, yrot and zrot
|
||||
ic1 = [ 0, 0, 1 ]; // north
|
||||
ic2 = yrot(ic1); // north and +x
|
||||
ic3 = zrot(ic2); // north and +x and +y
|
||||
ic4 = zrot(ic3); // north and -x and +y
|
||||
ic5 = zrot(ic4); // north and -x and -y
|
||||
ic6 = zrot(ic5); // north and +x and -y
|
||||
ic12 = [ 0, 0, -1]; // south
|
||||
ic10 = yrot(ic12); // south and -x
|
||||
ic11 = zrot(ic10); // south and -x and -y
|
||||
ic7 = zrot(ic11); // south and +x and -y
|
||||
ic8 = zrot(ic7); // south and +x and +y
|
||||
ic9 = zrot(ic8); // south and -x and +y
|
||||
|
||||
// start with icosahedron, icos[0] is vertices and icos[1] is faces
|
||||
icos = [ [ic1, ic2, ic3, ic4, ic5, ic6, ic7, ic8, ic9, ic10, ic11, ic12 ],
|
||||
[ [0, 2, 1], [0, 3, 2], [0, 4, 3], [0, 5, 4], [0, 1, 5],
|
||||
[1, 2, 7], [2, 3, 8], [3, 4, 9], [4, 5, 10], [5, 1, 6],
|
||||
[7, 6, 1], [8, 7, 2], [9, 8, 3], [10, 9, 4], [6, 10, 5],
|
||||
[6, 7, 11], [7, 8, 11], [8, 9, 11], [9, 10, 11], [10, 6, 11]]];
|
||||
|
||||
// now for polyhedron subdivision functions
|
||||
|
||||
// given two 3D points on the unit sphere, find the half-way point on the great circle
|
||||
// (euclidean midpoint renormalized to be 1 unit away from origin)
|
||||
function midpt(p1, p2) =
|
||||
let (midx = (p1[0] + p2[0])/2, midy = (p1[1] + p2[1])/2, midz = (p1[2] + p2[2])/2)
|
||||
let (midlen = sqrt(midx*midx + midy*midy + midz*midz))
|
||||
[ midx/midlen, midy/midlen, midz/midlen ];
|
||||
|
||||
// given a "struct" where pf[0] is vertices and pf[1] is faces, subdivide all faces into
|
||||
// 4 faces by dividing each edge in half along a great circle (midpt function)
|
||||
// and returns a struct of the same format, i.e. pf[0] is a (larger) list of vertices and
|
||||
// pf[1] is a larger list of faces.
|
||||
function subdivpf(pf) =
|
||||
let (p=pf[0], faces=pf[1])
|
||||
[ // for each face, barf out six points
|
||||
[ for (f=faces)
|
||||
let (p0 = p[f[0]], p1 = p[f[1]], p2=p[f[2]])
|
||||
// "identity" for-loop saves having to flatten
|
||||
for (outp=[ p0, p1, p2, midpt(p0, p1), midpt(p1, p2), midpt(p0, p2) ]) outp
|
||||
],
|
||||
// now, again for each face, spit out four faces that connect those six points
|
||||
[ for (i=[0:len(faces)-1])
|
||||
let (base = 6*i) // points generated in multiples of 6
|
||||
for (outf =
|
||||
[[ base, base+3, base+5],
|
||||
[base+3, base+1, base+4],
|
||||
[base+5, base+4, base+2],
|
||||
[base+3, base+4, base+5]]) outf // "identity" for-loop saves having to flatten
|
||||
]
|
||||
];
|
||||
|
||||
// recursive wrapper for subdivpf that subdivides "levels" times
|
||||
function multi_subdiv_pf(pf, levels) =
|
||||
levels == 0 ? pf :
|
||||
multi_subdiv_pf(subdivpf(pf), levels-1);
|
||||
|
||||
// subdivision level based on $fa:
|
||||
// level 0 has edge angle of edge_subtend so subdivision factor should be edge_subtend/$fa
|
||||
// must round up to next power of 2.
|
||||
// Take log base 2 of angle ratio and round up to next integer
|
||||
ang_levels = ceil(log(edge_subtend/$fa)/log(2));
|
||||
|
||||
// subdivision level based on $fs:
|
||||
// icosahedron edge length is rad*2*tan(edge_subtend/2)
|
||||
// actually a chord and not circumference but let's say it's close enough
|
||||
// subdivision factor should be rad*2*tan(edge_subtend/2)/$fs
|
||||
side_levels = ceil(log(rad*2*tan(edge_subtend/2)/$fs)/log(2));
|
||||
|
||||
// subdivision level based on $fn: (fragments around circumference, not total facets)
|
||||
// icosahedron circumference around equator is about 5 (level 1 is exactly 10)
|
||||
// ratio of requested to equatorial segments is $fn/5
|
||||
// level of subdivison is log base 2 of $fn/5
|
||||
// round up to the next whole level so we get at least $fn
|
||||
facet_levels = ceil(log($fn/5)/log(2));
|
||||
|
||||
// $fn takes precedence, otherwise facet_levels is NaN (-inf) but it's ok
|
||||
// because it falls back to $fa or $fs, whichever translates to fewer levels
|
||||
levels = $fn ? facet_levels : min(ang_levels, side_levels);
|
||||
|
||||
// subdivide icosahedron by these levels
|
||||
subdiv_icos = multi_subdiv_pf(icos, levels);
|
||||
|
||||
scale(rad)
|
||||
polyhedron(points=subdiv_icos[0], faces=subdiv_icos[1]);
|
||||
}
|
||||
63
src/libraries/polyhedrons.scad
Normal file
63
src/libraries/polyhedrons.scad
Normal file
|
|
@ -0,0 +1,63 @@
|
|||
function cat(L1, L2) = [for (i=[0:len(L1)+len(L2)-1])
|
||||
i < len(L1)? L1[i] : L2[i-len(L1)]] ;
|
||||
|
||||
|
||||
module dish(type = "sphere", sides = 10, length = 10){
|
||||
|
||||
//TODO length scaling
|
||||
|
||||
function pointyDish(x,y) = (x == 0 || y == 0 || x== sides || y == sides ) ? 0 : abs(5-x) + abs(5-y);
|
||||
|
||||
/*
|
||||
matrix looks like this:
|
||||
[
|
||||
[0, 0, 0], [0, 1, 0], [0, 2, 0],
|
||||
[1, 0, 0], [1, 1, 0], [1, 2, 0],
|
||||
[2, 0, 0], [2, 1, 0], [2, 2, 0]
|
||||
]
|
||||
*/
|
||||
// row is how many verts are actually in a row
|
||||
row = sides + 1;
|
||||
|
||||
// first make an x-first matrix of points. (0,0), (1,0) etc
|
||||
matrix = cat([
|
||||
for ( y = [0 : sides], x = [ 0 : sides ]) [x, y, pointyDish(x,y)]
|
||||
], [[sides / 2, sides / 2, 0]]);
|
||||
|
||||
echo(matrix);
|
||||
|
||||
echo(matrix[121]);
|
||||
|
||||
echo(len(matrix));
|
||||
|
||||
translate([sides / 2, sides / 2, 0]) sphere(r=1);
|
||||
|
||||
// then make 2 faces for each set of four points: (0,1,4), (0,4,3)
|
||||
// sides - 1 because we are doing this fromt the bottom left corner and extending up and out 1 vertex
|
||||
// so the rightmost and topmost vertexes are already covered
|
||||
f1 = [
|
||||
for (y = [0 : sides-1], x = [ 0 : sides-1 ], num = [0, 1]) (
|
||||
num == 0 ?
|
||||
[(x + row * y), (x + row * y + 1), (x + row * y + 1 + row)] :
|
||||
[(x + row * y), (x + row * y + 1 + row), (x + row * y + row)])
|
||||
];
|
||||
|
||||
f2 = cat(f1, [for (n = [0: sides-1]) [n, n+1, len(matrix) - 1]]);
|
||||
|
||||
faces = cat(f2, [for (n = [len(matrix) - sides-1 : len(matrix)]) [n-1, n, len(matrix) - 1]]);
|
||||
// add
|
||||
|
||||
/*
|
||||
faces needs to start like this:
|
||||
[
|
||||
[0,1,4,3],
|
||||
[1,2,5,4]
|
||||
]*/
|
||||
|
||||
/*index, index + 1, index + 1 + row, index + row*/
|
||||
|
||||
polyhedron(points = matrix, faces=faces);
|
||||
|
||||
}
|
||||
|
||||
dish();
|
||||
21
src/libraries/scad-utils/LICENSE
Normal file
21
src/libraries/scad-utils/LICENSE
Normal file
|
|
@ -0,0 +1,21 @@
|
|||
MIT License
|
||||
|
||||
Copyright (c) 2014 Oskar Linde
|
||||
|
||||
Permission is hereby granted, free of charge, to any person obtaining a copy
|
||||
of this software and associated documentation files (the "Software"), to deal
|
||||
in the Software without restriction, including without limitation the rights
|
||||
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
|
||||
copies of the Software, and to permit persons to whom the Software is
|
||||
furnished to do so, subject to the following conditions:
|
||||
|
||||
The above copyright notice and this permission notice shall be included in all
|
||||
copies or substantial portions of the Software.
|
||||
|
||||
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
|
||||
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
|
||||
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
|
||||
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
|
||||
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
|
||||
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
|
||||
SOFTWARE.
|
||||
81
src/libraries/scad-utils/README.md
Normal file
81
src/libraries/scad-utils/README.md
Normal file
|
|
@ -0,0 +1,81 @@
|
|||
scad-utils
|
||||
==========
|
||||
|
||||
Utility libraries for OpenSCAD
|
||||
|
||||
Morphology
|
||||
----------
|
||||
|
||||
contains basic 2D morphology operations
|
||||
|
||||
inset(d=1) - creates a polygon at an offset d inside a 2D shape
|
||||
outset(d=1) - creates a polygon at an offset d outside a 2D shape
|
||||
fillet(r=1) - adds fillets of radius r to all concave corners of a 2D shape
|
||||
rounding(r=1) - adds rounding to all convex corners of a 2D shape
|
||||
shell(d,center=false) - makes a shell of width d along the edge of a 2D shape
|
||||
- positive values of d places the shell on the outside
|
||||
- negative values of d places the shell on the inside
|
||||
- center=true and positive d places the shell centered on the edge
|
||||
|
||||
|
||||
### Examples
|
||||
|
||||
With a basic sample polygon shape,
|
||||
|
||||
module shape() {
|
||||
polygon([[0,0],[1,0],[1.5,1],[2.5,1],[2,-1],[0,-1]]);
|
||||
}
|
||||
|
||||
and `$fn=32;`.
|
||||
|
||||
|
||||
* `inset(d=0.3) shape();`
|
||||
|
||||

|
||||
|
||||
|
||||
* `outset(d=0.3) shape();`
|
||||
|
||||
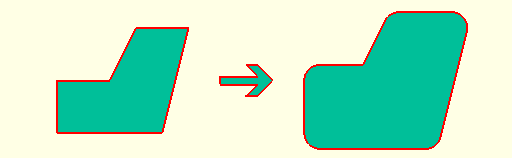
|
||||
|
||||
|
||||
* `rounding(r=0.3) shape();`
|
||||
|
||||
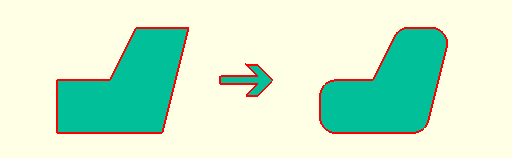
|
||||
|
||||
|
||||
* `fillet(r=0.3) shape();`
|
||||
|
||||
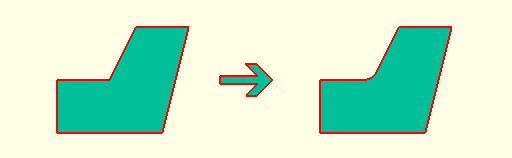
|
||||
|
||||
|
||||
*`shell(d=0.3) shape();`
|
||||
|
||||
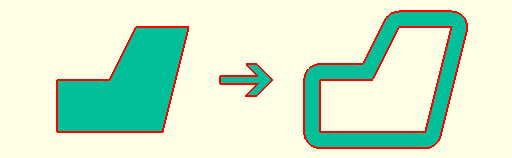
|
||||
|
||||
|
||||
*`shell(d=-0.3) shape();`
|
||||
|
||||
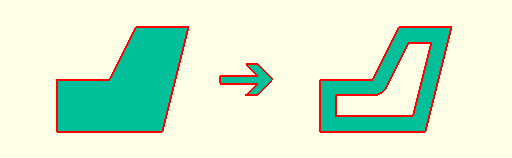
|
||||
|
||||
|
||||
*`shell(d=0.3,center=true) shape();`
|
||||
|
||||
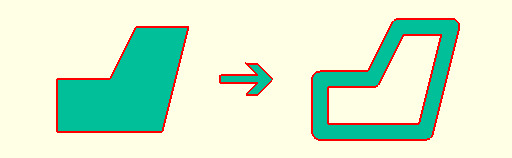
|
||||
|
||||
|
||||
Mirror
|
||||
------
|
||||
|
||||
contains simple mirroring functions
|
||||
|
||||
mirror_x()
|
||||
mirror_y()
|
||||
mirror_z()
|
||||
|
||||
example:
|
||||
|
||||
module arrow(l=1,w=.6,t=0.15) {
|
||||
mirror_y() polygon([[0,0],[l,0],[l-w/2,w/2],[l-w/2-sqrt(2)*t,w/2],[l-t/2-sqrt(2)*t,t/2],[0,t/2]]);
|
||||
}
|
||||
|
||||
324
src/libraries/scad-utils/hull.scad
Normal file
324
src/libraries/scad-utils/hull.scad
Normal file
|
|
@ -0,0 +1,324 @@
|
|||
|
||||
// NOTE: this code uses
|
||||
// * experimental let() syntax
|
||||
// * experimental list comprehension syntax
|
||||
// * search() bugfix and feature addition
|
||||
// * vector min()/max()
|
||||
|
||||
// Calculates the convex hull of a set of points.
|
||||
// The result is expressed in point indices.
|
||||
// If the points are collinear (or 2d), the result is a convex
|
||||
// polygon [i1,i2,i3,...], otherwise a triangular
|
||||
// polyhedron [[i1,i2,i3],[i2,i3,i4],...]
|
||||
|
||||
function hull(points) =
|
||||
!(len(points) > 0) ? [] :
|
||||
len(points[0]) == 2 ? convexhull2d(points) :
|
||||
len(points[0]) == 3 ? convexhull3d(points) : [];
|
||||
|
||||
epsilon = 1e-9;
|
||||
|
||||
// 2d version
|
||||
function convexhull2d(points) =
|
||||
len(points) < 3 ? [] : let(
|
||||
a=0, b=1,
|
||||
|
||||
c = find_first_noncollinear([a,b], points, 2)
|
||||
|
||||
) c == len(points) ? convexhull_collinear(points) : let(
|
||||
|
||||
remaining = [ for (i = [2:len(points)-1]) if (i != c) i ],
|
||||
|
||||
polygon = area_2d(points[a], points[b], points[c]) > 0 ? [a,b,c] : [b,a,c]
|
||||
|
||||
) convex_hull_iterative_2d(points, polygon, remaining);
|
||||
|
||||
|
||||
// Adds the remaining points one by one to the convex hull
|
||||
function convex_hull_iterative_2d(points, polygon, remaining, i_=0) = i_ >= len(remaining) ? polygon :
|
||||
let (
|
||||
// pick a point
|
||||
i = remaining[i_],
|
||||
|
||||
// find the segments that are in conflict with the point (point not inside)
|
||||
conflicts = find_conflicting_segments(points, polygon, points[i])
|
||||
|
||||
// no conflicts, skip point and move on
|
||||
) len(conflicts) == 0 ? convex_hull_iterative_2d(points, polygon, remaining, i_+1) : let(
|
||||
|
||||
// find the first conflicting segment and the first not conflicting
|
||||
// conflict will be sorted, if not wrapping around, do it the easy way
|
||||
polygon = remove_conflicts_and_insert_point(polygon, conflicts, i)
|
||||
) convex_hull_iterative_2d(
|
||||
points,
|
||||
polygon,
|
||||
remaining,
|
||||
i_+1
|
||||
);
|
||||
|
||||
function find_conflicting_segments(points, polygon, point) = [
|
||||
for (i = [0:len(polygon)-1]) let(j = (i+1) % len(polygon))
|
||||
if (area_2d(points[polygon[i]], points[polygon[j]], point) < 0)
|
||||
i
|
||||
];
|
||||
|
||||
// remove the conflicting segments from the polygon
|
||||
function remove_conflicts_and_insert_point(polygon, conflicts, point) =
|
||||
conflicts[0] == 0 ? let(
|
||||
nonconflicting = [ for(i = [0:len(polygon)-1]) if (!contains(conflicts, i)) i ],
|
||||
new_indices = concat(nonconflicting, (nonconflicting[len(nonconflicting)-1]+1) % len(polygon)),
|
||||
polygon = concat([ for (i = new_indices) polygon[i] ], point)
|
||||
) polygon : let(
|
||||
prior_to_first_conflict = [ for(i = [0:1:min(conflicts)]) polygon[i] ],
|
||||
after_last_conflict = [ for(i = [max(conflicts)+1:1:len(polygon)-1]) polygon[i] ],
|
||||
polygon = concat(prior_to_first_conflict, point, after_last_conflict)
|
||||
) polygon;
|
||||
|
||||
|
||||
// 3d version
|
||||
function convexhull3d(points) =
|
||||
len(points) < 3 ? [ for(i = [0:1:len(points)-1]) i ] : let (
|
||||
|
||||
// start with a single triangle
|
||||
a=0, b=1, c=2,
|
||||
plane = plane(points,a,b,c),
|
||||
|
||||
d = find_first_noncoplanar(plane, points, 3)
|
||||
|
||||
) d == len(points) ? /* all coplanar*/ let (
|
||||
|
||||
pts2d = [ for (p = points) plane_project(p, points[a], points[b], points[c]) ],
|
||||
hull2d = convexhull2d(pts2d)
|
||||
|
||||
) hull2d : let(
|
||||
|
||||
remaining = [for (i = [3:len(points)-1]) if (i != d) i],
|
||||
|
||||
// Build an initial tetrahedron
|
||||
|
||||
// swap b,c if d is in front of triangle t
|
||||
bc = in_front(plane, points[d]) ? [c,b] : [b,c],
|
||||
b = bc[0], c = bc[1],
|
||||
|
||||
triangles = [
|
||||
[a,b,c],
|
||||
[d,b,a],
|
||||
[c,d,a],
|
||||
[b,d,c],
|
||||
],
|
||||
|
||||
// calculate the plane equations
|
||||
planes = [ for (t = triangles) plane(points, t[0], t[1], t[2]) ]
|
||||
|
||||
) convex_hull_iterative(points, triangles, planes, remaining);
|
||||
|
||||
// A plane equation (normal, offset)
|
||||
function plane(points, a, b, c) = let(
|
||||
normal = unit(cross(points[c]-points[a], points[b]-points[a]))
|
||||
) [
|
||||
normal,
|
||||
normal * points[a]
|
||||
];
|
||||
|
||||
// Adds the remaining points one by one to the convex hull
|
||||
function convex_hull_iterative(points, triangles, planes, remaining, i_=0) = i_ >= len(remaining) ? triangles :
|
||||
let (
|
||||
// pick a point
|
||||
i = remaining[i_],
|
||||
|
||||
// find the triangles that are in conflict with the point (point not inside)
|
||||
conflicts = find_conflicts(points[i], planes),
|
||||
|
||||
// for all triangles that are in conflict, collect their halfedges
|
||||
halfedges = [
|
||||
for(c = conflicts)
|
||||
for(i = [0:2]) let(j = (i+1)%3)
|
||||
[triangles[c][i], triangles[c][j]]
|
||||
],
|
||||
|
||||
// find the outer perimeter of the set of conflicting triangles
|
||||
horizon = remove_internal_edges(halfedges),
|
||||
|
||||
// generate a new triangle for each horizon halfedge together with the picked point i
|
||||
new_triangles = [ for (h = horizon) concat(h,i) ],
|
||||
|
||||
// calculate the corresponding plane equations
|
||||
new_planes = [ for (t = new_triangles) plane(points, t[0], t[1], t[2]) ]
|
||||
|
||||
) convex_hull_iterative(
|
||||
points,
|
||||
// remove the conflicting triangles and add the new ones
|
||||
concat(remove_elements(triangles, conflicts), new_triangles),
|
||||
concat(remove_elements(planes, conflicts), new_planes),
|
||||
remaining,
|
||||
i_+1
|
||||
);
|
||||
|
||||
function convexhull_collinear(points) = let(
|
||||
n = points[1] - points[0],
|
||||
a = points[0],
|
||||
points1d = [ for(p = points) (p-a)*n ],
|
||||
min_i = min_index(points1d),
|
||||
max_i = max_index(points1d)
|
||||
) [ min_i, max_i ];
|
||||
|
||||
function min_index(values,min_,min_i_,i_) =
|
||||
i_ == undef ? min_index(values,values[0],0,1) :
|
||||
i_ >= len(values) ? min_i_ :
|
||||
values[i_] < min_ ? min_index(values,values[i_],i_,i_+1)
|
||||
: min_index(values,min_,min_i_,i_+1);
|
||||
|
||||
function max_index(values,max_,max_i_,i_) =
|
||||
i_ == undef ? max_index(values,values[0],0,1) :
|
||||
i_ >= len(values) ? max_i_ :
|
||||
values[i_] > max_ ? max_index(values,values[i_],i_,i_+1)
|
||||
: max_index(values,max_,max_i_,i_+1);
|
||||
|
||||
function remove_elements(array, elements) = [
|
||||
for (i = [0:len(array)-1])
|
||||
if (!search(i, elements))
|
||||
array[i]
|
||||
];
|
||||
|
||||
function remove_internal_edges(halfedges) = [
|
||||
for (h = halfedges)
|
||||
if (!contains(halfedges, reverse(h)))
|
||||
h
|
||||
];
|
||||
|
||||
function plane_project(point, a, b, c) = let(
|
||||
u = b-a,
|
||||
v = c-a,
|
||||
n = cross(u,v),
|
||||
w = cross(n,u),
|
||||
relpoint = point-a
|
||||
) [relpoint * u, relpoint * w];
|
||||
|
||||
function plane_unproject(point, a, b, c) = let(
|
||||
u = b-a,
|
||||
v = c-a,
|
||||
n = cross(u,v),
|
||||
w = cross(n,u)
|
||||
) a + point[0] * u + point[1] * w;
|
||||
|
||||
function reverse(arr) = [ for (i = [len(arr)-1:-1:0]) arr[i] ];
|
||||
|
||||
function contains(arr, element) = search([element],arr)[0] != [] ? true : false;
|
||||
|
||||
function find_conflicts(point, planes) = [
|
||||
for (i = [0:len(planes)-1])
|
||||
if (in_front(planes[i], point))
|
||||
i
|
||||
];
|
||||
|
||||
function find_first_noncollinear(line, points, i) =
|
||||
i >= len(points) ? len(points) :
|
||||
collinear(points[line[0]],
|
||||
points[line[1]],
|
||||
points[i]) ? find_first_noncollinear(line, points, i+1)
|
||||
: i;
|
||||
|
||||
function find_first_noncoplanar(plane, points, i) =
|
||||
i >= len(points) ? len(points) :
|
||||
coplanar(plane, points[i]) ? find_first_noncoplanar(plane, points, i+1)
|
||||
: i;
|
||||
|
||||
function distance(plane, point) = plane[0] * point - plane[1];
|
||||
|
||||
function in_front(plane, point) = distance(plane, point) > epsilon;
|
||||
|
||||
function coplanar(plane, point) = abs(distance(plane,point)) <= epsilon;
|
||||
|
||||
function unit(v) = v/norm(v);
|
||||
|
||||
function area_2d(a,b,c) = (
|
||||
a[0] * (b[1] - c[1]) +
|
||||
b[0] * (c[1] - a[1]) +
|
||||
c[0] * (a[1] - b[1])) / 2;
|
||||
|
||||
function collinear(a,b,c) = abs(area_2d(a,b,c)) < epsilon;
|
||||
|
||||
function spherical(cartesian) = [
|
||||
atan2(cartesian[1], cartesian[0]),
|
||||
asin(cartesian[2])
|
||||
];
|
||||
|
||||
function cartesian(spherical) = [
|
||||
cos(spherical[1]) * cos(spherical[0]),
|
||||
cos(spherical[1]) * sin(spherical[0]),
|
||||
sin(spherical[1])
|
||||
];
|
||||
|
||||
|
||||
/// TESTCODE
|
||||
|
||||
|
||||
phi = 1.618033988749895;
|
||||
|
||||
testpoints_on_sphere = [ for(p =
|
||||
[
|
||||
[1,phi,0], [-1,phi,0], [1,-phi,0], [-1,-phi,0],
|
||||
[0,1,phi], [0,-1,phi], [0,1,-phi], [0,-1,-phi],
|
||||
[phi,0,1], [-phi,0,1], [phi,0,-1], [-phi,0,-1]
|
||||
])
|
||||
unit(p)
|
||||
];
|
||||
|
||||
testpoints_spherical = [ for(p = testpoints_on_sphere) spherical(p) ];
|
||||
testpoints_circular = [ for(a = [0:15:360-epsilon]) [cos(a),sin(a)] ];
|
||||
|
||||
testpoints_coplanar = let(u = unit([1,3,7]), v = unit([-2,1,-2])) [ for(i = [1:10]) rands(-1,1,1)[0] * u + rands(-1,1,1)[0] * v ];
|
||||
|
||||
testpoints_collinear_2d = let(u = unit([5,3])) [ for(i = [1:20]) rands(-1,1,1)[0] * u ];
|
||||
testpoints_collinear_3d = let(u = unit([5,3,-5])) [ for(i = [1:20]) rands(-1,1,1)[0] * u ];
|
||||
|
||||
testpoints2d = 20 * [for (i = [1:10]) concat(rands(-1,1,2))];
|
||||
testpoints3d = 20 * [for (i = [1:50]) concat(rands(-1,1,3))];
|
||||
|
||||
// All points are on the sphere, no point should be red
|
||||
translate([-50,0]) visualize_hull(20*testpoints_on_sphere);
|
||||
|
||||
// 2D points
|
||||
translate([50,0]) visualize_hull(testpoints2d);
|
||||
|
||||
// All points on a circle, no point should be red
|
||||
translate([0,50]) visualize_hull(20*testpoints_circular);
|
||||
|
||||
// All points 3d but collinear
|
||||
translate([0,-50]) visualize_hull(20*testpoints_coplanar);
|
||||
|
||||
// Collinear
|
||||
translate([50,50]) visualize_hull(20*testpoints_collinear_2d);
|
||||
|
||||
// Collinear
|
||||
translate([-50,50]) visualize_hull(20*testpoints_collinear_3d);
|
||||
|
||||
// 3D points
|
||||
visualize_hull(testpoints3d);
|
||||
|
||||
|
||||
module visualize_hull(points) {
|
||||
|
||||
hull = hull(points);
|
||||
|
||||
%if (len(hull) > 0 && len(hull[0]) > 0)
|
||||
polyhedron(points=points, faces = hull);
|
||||
else
|
||||
polyhedron(points=points, faces = [hull]);
|
||||
|
||||
for (i = [0:len(points)-1]) assign(p = points[i], $fn = 16) {
|
||||
translate(p) {
|
||||
if (hull_contains_index(hull,i)) {
|
||||
color("blue") sphere(1);
|
||||
} else {
|
||||
color("red") sphere(1);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
function hull_contains_index(hull, index) =
|
||||
search(index,hull,1,0) ||
|
||||
search(index,hull,1,1) ||
|
||||
search(index,hull,1,2);
|
||||
|
||||
}
|
||||
32
src/libraries/scad-utils/linalg.scad
Normal file
32
src/libraries/scad-utils/linalg.scad
Normal file
|
|
@ -0,0 +1,32 @@
|
|||
// very minimal set of linalg functions needed by so3, se3 etc.
|
||||
|
||||
// cross and norm are builtins
|
||||
//function cross(x,y) = [x[1]*y[2]-x[2]*y[1], x[2]*y[0]-x[0]*y[2], x[0]*y[1]-x[1]*y[0]];
|
||||
//function norm(v) = sqrt(v*v);
|
||||
|
||||
function vec3(p) = len(p) < 3 ? concat(p,0) : p;
|
||||
function vec4(p) = let (v3=vec3(p)) len(v3) < 4 ? concat(v3,1) : v3;
|
||||
function unit(v) = v/norm(v);
|
||||
|
||||
function identity3()=[[1,0,0],[0,1,0],[0,0,1]];
|
||||
function identity4()=[[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]];
|
||||
|
||||
|
||||
function take3(v) = [v[0],v[1],v[2]];
|
||||
function tail3(v) = [v[3],v[4],v[5]];
|
||||
function rotation_part(m) = [take3(m[0]),take3(m[1]),take3(m[2])];
|
||||
function rot_trace(m) = m[0][0] + m[1][1] + m[2][2];
|
||||
function rot_cos_angle(m) = (rot_trace(m)-1)/2;
|
||||
|
||||
function rotation_part(m) = [take3(m[0]),take3(m[1]),take3(m[2])];
|
||||
function translation_part(m) = [m[0][3],m[1][3],m[2][3]];
|
||||
function transpose_3(m) = [[m[0][0],m[1][0],m[2][0]],[m[0][1],m[1][1],m[2][1]],[m[0][2],m[1][2],m[2][2]]];
|
||||
function transpose_4(m) = [[m[0][0],m[1][0],m[2][0],m[3][0]],
|
||||
[m[0][1],m[1][1],m[2][1],m[3][1]],
|
||||
[m[0][2],m[1][2],m[2][2],m[3][2]],
|
||||
[m[0][3],m[1][3],m[2][3],m[3][3]]];
|
||||
function invert_rt(m) = construct_Rt(transpose_3(rotation_part(m)), -(transpose_3(rotation_part(m)) * translation_part(m)));
|
||||
function construct_Rt(R,t) = [concat(R[0],t[0]),concat(R[1],t[1]),concat(R[2],t[2]),[0,0,0,1]];
|
||||
|
||||
// Hadamard product of n-dimensional arrays
|
||||
function hadamard(a,b) = !(len(a)>0) ? a*b : [ for(i = [0:len(a)-1]) hadamard(a[i],b[i]) ];
|
||||
48
src/libraries/scad-utils/lists.scad
Normal file
48
src/libraries/scad-utils/lists.scad
Normal file
|
|
@ -0,0 +1,48 @@
|
|||
// List helpers
|
||||
|
||||
/*!
|
||||
Flattens a list one level:
|
||||
|
||||
flatten([[0,1],[2,3]]) => [0,1,2,3]
|
||||
*/
|
||||
function flatten(list) = [ for (i = list, v = i) v ];
|
||||
|
||||
|
||||
/*!
|
||||
Creates a list from a range:
|
||||
|
||||
range([0:2:6]) => [0,2,4,6]
|
||||
*/
|
||||
function range(r) = [ for(x=r) x ];
|
||||
|
||||
/*!
|
||||
Reverses a list:
|
||||
|
||||
reverse([1,2,3]) => [3,2,1]
|
||||
*/
|
||||
function reverse(list) = [for (i = [len(list)-1:-1:0]) list[i]];
|
||||
|
||||
/*!
|
||||
Extracts a subarray from index begin (inclusive) to end (exclusive)
|
||||
FIXME: Change name to use list instead of array?
|
||||
|
||||
subarray([1,2,3,4], 1, 2) => [2,3]
|
||||
*/
|
||||
function subarray(list,begin=0,end=-1) = [
|
||||
let(end = end < 0 ? len(list) : end)
|
||||
for (i = [begin : 1 : end-1])
|
||||
list[i]
|
||||
];
|
||||
|
||||
/*!
|
||||
Returns a copy of a list with the element at index i set to x
|
||||
|
||||
set([1,2,3,4], 2, 5) => [1,2,5,4]
|
||||
*/
|
||||
function set(list, i, x) = [for (i_=[0:len(list)-1]) i == i_ ? x : list[i_]];
|
||||
|
||||
/*!
|
||||
Remove element from the list by index.
|
||||
remove([4,3,2,1],1) => [4,2,1]
|
||||
*/
|
||||
function remove(list, i) = [for (i_=[0:1:len(list)-2]) list[i_ < i ? i_ : i_ + 1]];
|
||||
30
src/libraries/scad-utils/mirror.scad
Normal file
30
src/libraries/scad-utils/mirror.scad
Normal file
|
|
@ -0,0 +1,30 @@
|
|||
// Copyright (c) 2013 Oskar Linde. All rights reserved.
|
||||
// License: BSD
|
||||
//
|
||||
// This library contains simple mirroring functions
|
||||
//
|
||||
// mirror_x()
|
||||
// mirror_y()
|
||||
// mirror_z()
|
||||
|
||||
|
||||
module mirror_x() {
|
||||
union() {
|
||||
child();
|
||||
scale([-1,1,1]) child();
|
||||
}
|
||||
}
|
||||
|
||||
module mirror_y() {
|
||||
union() {
|
||||
child();
|
||||
scale([1,-1,1]) child();
|
||||
}
|
||||
}
|
||||
|
||||
module mirror_z() {
|
||||
union() {
|
||||
child();
|
||||
scale([1,1,-1]) child();
|
||||
}
|
||||
}
|
||||
109
src/libraries/scad-utils/morphology.scad
Normal file
109
src/libraries/scad-utils/morphology.scad
Normal file
|
|
@ -0,0 +1,109 @@
|
|||
// Copyright (c) 2013 Oskar Linde. All rights reserved.
|
||||
// License: BSD
|
||||
//
|
||||
// This library contains basic 2D morphology operations
|
||||
//
|
||||
// outset(d=1) - creates a polygon at an offset d outside a 2D shape
|
||||
// inset(d=1) - creates a polygon at an offset d inside a 2D shape
|
||||
// fillet(r=1) - adds fillets of radius r to all concave corners of a 2D shape
|
||||
// rounding(r=1) - adds rounding to all convex corners of a 2D shape
|
||||
// shell(d,center=false) - makes a shell of width d along the edge of a 2D shape
|
||||
// - positive values of d places the shell on the outside
|
||||
// - negative values of d places the shell on the inside
|
||||
// - center=true and positive d places the shell centered on the edge
|
||||
|
||||
module outset(d=1) {
|
||||
// Bug workaround for older OpenSCAD versions
|
||||
if (version_num() < 20130424) render() outset_extruded(d) child();
|
||||
else minkowski() {
|
||||
circle(r=d);
|
||||
child();
|
||||
}
|
||||
}
|
||||
|
||||
module outset_extruded(d=1) {
|
||||
projection(cut=true) minkowski() {
|
||||
cylinder(r=d);
|
||||
linear_extrude(center=true) child();
|
||||
}
|
||||
}
|
||||
|
||||
module inset(d=1) {
|
||||
render() inverse() outset(d=d) inverse() child();
|
||||
}
|
||||
|
||||
module fillet(r=1) {
|
||||
inset(d=r) render() outset(d=r) child();
|
||||
}
|
||||
|
||||
module rounding(r=1) {
|
||||
outset(d=r) inset(d=r) child();
|
||||
}
|
||||
|
||||
module shell(d,center=false) {
|
||||
if (center && d > 0) {
|
||||
difference() {
|
||||
outset(d=d/2) child();
|
||||
inset(d=d/2) child();
|
||||
}
|
||||
}
|
||||
if (!center && d > 0) {
|
||||
difference() {
|
||||
outset(d=d) child();
|
||||
child();
|
||||
}
|
||||
}
|
||||
if (!center && d < 0) {
|
||||
difference() {
|
||||
child();
|
||||
inset(d=-d) child();
|
||||
}
|
||||
}
|
||||
if (d == 0) child();
|
||||
}
|
||||
|
||||
|
||||
// Below are for internal use only
|
||||
|
||||
module inverse() {
|
||||
difference() {
|
||||
square(1e5,center=true);
|
||||
child();
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
// TEST CODE
|
||||
|
||||
use <mirror.scad>
|
||||
|
||||
module arrow(l=1,w=.6,t=0.15) {
|
||||
mirror_y() polygon([[0,0],[l,0],[l-w/2,w/2],[l-w/2-sqrt(2)*t,w/2],[l-t/2-sqrt(2)*t,t/2],[0,t/2]]);
|
||||
}
|
||||
|
||||
module shape() {
|
||||
polygon([[0,0],[1,0],[1.5,1],[2.5,1],[2,-1],[0,-1]]);
|
||||
}
|
||||
|
||||
if(0) assign($fn=32) {
|
||||
|
||||
for (p = [0:10*3-1]) assign(o=floor(p/3)) {
|
||||
translate([(p%3)*2.5,-o*3]) {
|
||||
//%if (p % 3 == 1) translate([0,0,1]) shape();
|
||||
if (p % 3 == 0) shape();
|
||||
if (p % 3 == 1) translate([0.6,0]) arrow();
|
||||
if (p % 3 == 2) {
|
||||
if (o == 0) inset(d=0.3) shape();
|
||||
if (o == 1) outset(d=0.3) shape();
|
||||
if (o == 2) rounding(r=0.3) shape();
|
||||
if (o == 3) fillet(r=0.3) shape();
|
||||
if (o == 4) shell(d=0.3) shape();
|
||||
if (o == 5) shell(d=-0.3) shape();
|
||||
if (o == 6) shell(d=0.3,center=true) shape();
|
||||
if (o == 7) rounding(r=0.3) fillet(r=0.3) shape();
|
||||
if (o == 8) shell(d=0.3,center=true) fillet(r=0.3) rounding(r=0.3) shape();
|
||||
if (o == 9) shell(d=-0.3) fillet(r=0.3) rounding(r=0.3) shape();
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
60
src/libraries/scad-utils/se3.scad
Normal file
60
src/libraries/scad-utils/se3.scad
Normal file
|
|
@ -0,0 +1,60 @@
|
|||
use <linalg.scad>
|
||||
use <so3.scad>
|
||||
|
||||
function combine_se3_exp(w, ABt) = construct_Rt(rodrigues_so3_exp(w, ABt[0], ABt[1]), ABt[2]);
|
||||
|
||||
// [A,B,t]
|
||||
function se3_exp_1(t,w) = concat(
|
||||
so3_exp_1(w*w),
|
||||
[t + 0.5 * cross(w,t)]
|
||||
);
|
||||
|
||||
function se3_exp_2(t,w) = se3_exp_2_0(t,w,w*w);
|
||||
function se3_exp_2_0(t,w,theta_sq) =
|
||||
se3_exp_23(
|
||||
so3_exp_2(theta_sq),
|
||||
C = (1.0 - theta_sq/20) / 6,
|
||||
t=t,w=w);
|
||||
|
||||
function se3_exp_3(t,w) = se3_exp_3_0(t,w,sqrt(w*w)*180/PI,1/sqrt(w*w));
|
||||
|
||||
function se3_exp_3_0(t,w,theta_deg,inv_theta) =
|
||||
se3_exp_23(
|
||||
so3_exp_3_0(theta_deg = theta_deg, inv_theta = inv_theta),
|
||||
C = (1 - sin(theta_deg) * inv_theta) * (inv_theta * inv_theta),
|
||||
t=t,w=w);
|
||||
|
||||
function se3_exp_23(AB,C,t,w) =
|
||||
[AB[0], AB[1], t + AB[1] * cross(w,t) + C * cross(w,cross(w,t)) ];
|
||||
|
||||
function se3_exp(mu) = se3_exp_0(t=take3(mu),w=tail3(mu)/180*PI);
|
||||
|
||||
function se3_exp_0(t,w) =
|
||||
combine_se3_exp(w,
|
||||
// Evaluate by Taylor expansion when near 0
|
||||
w*w < 1e-8
|
||||
? se3_exp_1(t,w)
|
||||
: w*w < 1e-6
|
||||
? se3_exp_2(t,w)
|
||||
: se3_exp_3(t,w)
|
||||
);
|
||||
|
||||
function se3_ln(m) = se3_ln_to_deg(se3_ln_rad(m));
|
||||
function se3_ln_to_deg(v) = concat(take3(v),tail3(v)*180/PI);
|
||||
|
||||
function se3_ln_rad(m) = se3_ln_0(m,
|
||||
rot = so3_ln_rad(rotation_part(m)));
|
||||
function se3_ln_0(m,rot) = se3_ln_1(m,rot,
|
||||
theta = sqrt(rot*rot));
|
||||
function se3_ln_1(m,rot,theta) = se3_ln_2(m,rot,theta,
|
||||
shtot = theta > 0.00001 ? sin(theta/2*180/PI)/theta : 0.5,
|
||||
halfrotator = so3_exp_rad(rot * -.5));
|
||||
function se3_ln_2(m,rot,theta,shtot,halfrotator) =
|
||||
concat( (halfrotator * translation_part(m) -
|
||||
(theta > 0.001
|
||||
? rot * ((translation_part(m) * rot) * (1-2*shtot) / (rot*rot))
|
||||
: rot * ((translation_part(m) * rot)/24)
|
||||
)) / (2 * shtot), rot);
|
||||
|
||||
__se3_test = [20,-40,60,-80,100,-120];
|
||||
echo(UNITTEST_se3=norm(__se3_test-se3_ln(se3_exp(__se3_test))) < 1e-8);
|
||||
16
src/libraries/scad-utils/shapes.scad
Normal file
16
src/libraries/scad-utils/shapes.scad
Normal file
|
|
@ -0,0 +1,16 @@
|
|||
function square(size) = [[-size,-size], [-size,size], [size,size], [size,-size]] / 2;
|
||||
|
||||
function circle(r) = [for (i=[0:$fn-1]) let (a=i*360/$fn) r * [cos(a), sin(a)]];
|
||||
|
||||
function regular(r, n) = circle(r, $fn=n);
|
||||
|
||||
function rectangle_profile(size=[1,1]) = [
|
||||
// The first point is the anchor point, put it on the point corresponding to [cos(0),sin(0)]
|
||||
[ size[0]/2, 0],
|
||||
[ size[0]/2, size[1]/2],
|
||||
[-size[0]/2, size[1]/2],
|
||||
[-size[0]/2, -size[1]/2],
|
||||
[ size[0]/2, -size[1]/2],
|
||||
];
|
||||
|
||||
// FIXME: Move rectangle and rounded rectangle from extrusion
|
||||
82
src/libraries/scad-utils/so3.scad
Normal file
82
src/libraries/scad-utils/so3.scad
Normal file
|
|
@ -0,0 +1,82 @@
|
|||
// so3
|
||||
|
||||
use <linalg.scad>
|
||||
|
||||
function rodrigues_so3_exp(w, A, B) = [
|
||||
[1.0 - B*(w[1]*w[1] + w[2]*w[2]), B*(w[0]*w[1]) - A*w[2], B*(w[0]*w[2]) + A*w[1]],
|
||||
[B*(w[0]*w[1]) + A*w[2], 1.0 - B*(w[0]*w[0] + w[2]*w[2]), B*(w[1]*w[2]) - A*w[0]],
|
||||
[B*(w[0]*w[2]) - A*w[1], B*(w[1]*w[2]) + A*w[0], 1.0 - B*(w[0]*w[0] + w[1]*w[1])]
|
||||
];
|
||||
|
||||
function so3_exp(w) = so3_exp_rad(w/180*PI);
|
||||
function so3_exp_rad(w) =
|
||||
combine_so3_exp(w,
|
||||
w*w < 1e-8
|
||||
? so3_exp_1(w*w)
|
||||
: w*w < 1e-6
|
||||
? so3_exp_2(w*w)
|
||||
: so3_exp_3(w*w));
|
||||
|
||||
function combine_so3_exp(w,AB) = rodrigues_so3_exp(w,AB[0],AB[1]);
|
||||
|
||||
// Taylor series expansions close to 0
|
||||
function so3_exp_1(theta_sq) = [
|
||||
1 - 1/6*theta_sq,
|
||||
0.5
|
||||
];
|
||||
|
||||
function so3_exp_2(theta_sq) = [
|
||||
1.0 - theta_sq * (1.0 - theta_sq/20) / 6,
|
||||
0.5 - 0.25/6 * theta_sq
|
||||
];
|
||||
|
||||
function so3_exp_3_0(theta_deg, inv_theta) = [
|
||||
sin(theta_deg) * inv_theta,
|
||||
(1 - cos(theta_deg)) * (inv_theta * inv_theta)
|
||||
];
|
||||
|
||||
function so3_exp_3(theta_sq) = so3_exp_3_0(sqrt(theta_sq)*180/PI, 1/sqrt(theta_sq));
|
||||
|
||||
|
||||
function rot_axis_part(m) = [m[2][1] - m[1][2], m[0][2] - m[2][0], m[1][0] - m[0][1]]*0.5;
|
||||
|
||||
function so3_ln(m) = 180/PI*so3_ln_rad(m);
|
||||
function so3_ln_rad(m) = so3_ln_0(m,
|
||||
cos_angle = rot_cos_angle(m),
|
||||
preliminary_result = rot_axis_part(m));
|
||||
|
||||
function so3_ln_0(m, cos_angle, preliminary_result) =
|
||||
so3_ln_1(m, cos_angle, preliminary_result,
|
||||
sin_angle_abs = sqrt(preliminary_result*preliminary_result));
|
||||
|
||||
function so3_ln_1(m, cos_angle, preliminary_result, sin_angle_abs) =
|
||||
cos_angle > sqrt(1/2)
|
||||
? sin_angle_abs > 0
|
||||
? preliminary_result * asin(sin_angle_abs)*PI/180 / sin_angle_abs
|
||||
: preliminary_result
|
||||
: cos_angle > -sqrt(1/2)
|
||||
? preliminary_result * acos(cos_angle)*PI/180 / sin_angle_abs
|
||||
: so3_get_symmetric_part_rotation(
|
||||
preliminary_result,
|
||||
m,
|
||||
angle = PI - asin(sin_angle_abs)*PI/180,
|
||||
d0 = m[0][0] - cos_angle,
|
||||
d1 = m[1][1] - cos_angle,
|
||||
d2 = m[2][2] - cos_angle
|
||||
);
|
||||
|
||||
function so3_get_symmetric_part_rotation(preliminary_result, m, angle, d0, d1, d2) =
|
||||
so3_get_symmetric_part_rotation_0(preliminary_result,angle,so3_largest_column(m, d0, d1, d2));
|
||||
|
||||
function so3_get_symmetric_part_rotation_0(preliminary_result, angle, c_max) =
|
||||
angle * unit(c_max * preliminary_result < 0 ? -c_max : c_max);
|
||||
|
||||
function so3_largest_column(m, d0, d1, d2) =
|
||||
d0*d0 > d1*d1 && d0*d0 > d2*d2
|
||||
? [d0, (m[1][0]+m[0][1])/2, (m[0][2]+m[2][0])/2]
|
||||
: d1*d1 > d2*d2
|
||||
? [(m[1][0]+m[0][1])/2, d1, (m[2][1]+m[1][2])/2]
|
||||
: [(m[0][2]+m[2][0])/2, (m[2][1]+m[1][2])/2, d2];
|
||||
|
||||
__so3_test = [12,-125,110];
|
||||
echo(UNITTEST_so3=norm(__so3_test-so3_ln(so3_exp(__so3_test))) < 1e-8);
|
||||
113
src/libraries/scad-utils/spline.scad
Normal file
113
src/libraries/scad-utils/spline.scad
Normal file
|
|
@ -0,0 +1,113 @@
|
|||
// Spline module for scad-util library
|
||||
// Author Sergei Kuzmin, 2014.
|
||||
|
||||
// For n+1 given point and hense n intervals returns the spline coefficient matrix.
|
||||
// param p defines the anchor points.
|
||||
// File defines two functions: spline_args and spline.
|
||||
// example usage:
|
||||
// spl1 = spline_args(point, v1=[0,1,0], closed=false);
|
||||
// interpolated_points = [for(t=[0:0.1:len(point)-1]) spline(spl1, t)]
|
||||
|
||||
use <linalg.scad>
|
||||
use <lists.scad>
|
||||
|
||||
q1=[[1,0,0,0],[1,1,1,1],[0,1,2,3],[0,0,1,3]];
|
||||
q1inv=[[1,0,0,0],[-3,3,-2,1],[3,-3,3,-2],[-1,1,-1,1]];
|
||||
q2=[[0,0,0,0],[0,0,0,0],[0,-1,0,0],[0,0,-1,0]];
|
||||
qn1i2=-q1inv*q2;
|
||||
z3=[0,0,0];
|
||||
z4=[0,0,0,0];
|
||||
|
||||
function matrix_power(m,n)= n==0? (len(m)==3?identity3():identity4()) :
|
||||
n==1 ? m : (n%2==1) ? matrix_power(m*m,floor(n/2))*m : matrix_power(m*m,n/2);
|
||||
|
||||
function det(m) = let(r=[for(i=[0:1:len(m)-1]) i]) det_help(m, 0, r);
|
||||
// Construction indices list is inefficient, but currently there is no way to imperatively
|
||||
// assign to a list element
|
||||
function det_help(m, i, r) = len(r) == 0 ? 1 :
|
||||
m[len(m)-len(r)][r[i]]*det_help(m,0,remove(r,i)) - (i+1<len(r)? det_help(m, i+1, r) : 0);
|
||||
|
||||
function matrix_invert(m) = let(r=[for(i=[0:len(m)-1]) i]) [for(i=r) [for(j=r)
|
||||
((i+j)%2==0 ? 1:-1) * matrix_minor(m,0,remove(r,j),remove(r,i))]] / det(m);
|
||||
function matrix_minor(m,k,ri, rj) = let(len_r=len(ri)) len_r == 0 ? 1 :
|
||||
m[ri[0]][rj[k]]*matrix_minor(m,0,remove(ri,0),remove(rj,k)) - (k+1<len_r?matrix_minor(m,k+1,ri,rj) : 0);
|
||||
|
||||
function spline_u(i,p) = [p[i],p[i+1],z3,z3];
|
||||
|
||||
function spline_args(p, closed=false, v1=undef, v2=undef)=len(p)<2 ? []:
|
||||
let(q3=closed?q2:[z4, z4, v1==undef?[0,0,1,0]:[0,1,0,0], z4],
|
||||
q4=closed?q1:[[1,0,0,0], [1,1,1,1], z4, v2==undef?[0,0,1,3]:[0,1,2,3]],
|
||||
pcnt=closed? len(p) + 1 : len(p),
|
||||
un=[p[pcnt-2],p[closed?0:pcnt-1],v1==undef?z4:v1, v2==undef?z4:v2],
|
||||
sn=matrix_invert(q4+q3*matrix_power(qn1i2,pcnt-2))*(un-q3*q1inv*spline_helper(0, pcnt, p)))
|
||||
// result[i+1] recurrently defines result[i]. This is O(n) runtime with imperative language and
|
||||
// may be O(n^2) if OpenSCAD doesn't cache spline_si(i+1).
|
||||
[for(i=[0:pcnt-2]) spline_si(i, pcnt-2, p, sn)];
|
||||
|
||||
// n is number of points including pseudopoint for closed contour
|
||||
// Weird construct cause there is no if statement for functions
|
||||
function spline_helper(i, n, p) = let(u=[p[i], p[i+1], z3, z3]) i+3>=n? u : u-q2*q1inv*spline_helper(i+1, n, p);
|
||||
|
||||
// knowing s[j+1], calculate s[j]. Stop when found s[i]
|
||||
function spline_si(i,n, p, sn) = i == n ? sn : q1inv*(spline_u(i,p)-q2*spline_si(i+1, n, p, sn));
|
||||
|
||||
// Takes array of (3n+1) points or (2n + 2) points, if tangent segments are symmetric.
|
||||
// For non-symmetric version input is: point0, normal0, neg_normal1, point1, normal1, ... neg_normal_n, point_n
|
||||
// For symmetric version: point0, normal0, point1, normal1, ... , normal_n_sub_1, point_n
|
||||
// In the second case second tangent is constructed from the next tangent by symmetric map.
|
||||
// I.e. if current points are p0,p1,p2 then anchor points are p0 and p2, first tangent defined by p1-p0,
|
||||
// second tangent defined by p3-p2.
|
||||
// Return array of coefficients accepted by spline(), spline_tan() and similar
|
||||
function bezier3_args(p, symmetric=false) = let(step=symmetric?2:3)
|
||||
[for(i=[0:step:len(p)-3]) [[1,0,0,0],[-3,3,0,0],[3,-6,3,0],[-1,3,-3,1]]*
|
||||
(symmetric?[p[i],p[i]+p[i+1],p[i+2]-p[i+3],p[i+2]] : [p[i], p[i]+p[i+1], p[i+3]+p[i+2], p[i+3]])];
|
||||
|
||||
// s - spline arguments calculated by spline_args
|
||||
// t - defines point on curve. each segment length is 1. I.e. t= 0..1 is first segment, t=1..2 - second.
|
||||
function spline(s, t)= let(i=t>=len(s)?len(s)-1: floor(t), t2=t-i) [1,t2,t2*t2,t2*t2*t2]*s[i];
|
||||
|
||||
function spline_tan(s, t)= let(i=t>=len(s)?len(s)-1: floor(t), t2=t-i) [0,1,2*t2,3*t2*t2]*s[i];
|
||||
function spline_tan_unit(s, t)= unit(spline_tan(s,t));
|
||||
function spline_d2(s,t)= let(i=t>=len(s)?len(s)-1: floor(t), t2=t-i) [0,0,2,6*t2]*s[i];
|
||||
function spline_binormal_unit(s,t)= unit(cross(spline_tan(s, t), spline_d2(s,t)));
|
||||
function spline_normal_unit(s,t)= unit(cross(spline_tan(s, t), spline_binormal_unit(s,t)));
|
||||
|
||||
function spline_transform(s, t)=
|
||||
construct_Rt(transpose_3([spline_normal_unit(s,t), spline_binormal_unit(s,t), spline_tan_unit(s,t)]), spline(s,t));
|
||||
|
||||
// Unit tests
|
||||
__s = spline_args([[0,10,0], [10,0,0],[0,-5,2]], v1=[0,1,0], v2=[-1,0,0], closed=true);
|
||||
for(t=[0:0.01:len(__s)]) translate(spline(__s, t))
|
||||
cube([0.2,0.2,0.2], center=true);
|
||||
|
||||
__s1=spline_args([[0,0,0],[0,0,15], [26,0,26+15]], /*v1=[0,0,100],*/ v2=[40,0,0]);
|
||||
for(t=[0:0.01:len(s1)]) translate(spline(__s1, t))
|
||||
cube([0.2,0.2,0.2], center=true);
|
||||
|
||||
__s2=bezier3_args([[0,0,0],[0,0,10],[0,0,15],[0,0,26*0.552284],[26,0,41],[26*0.552284,0,0]],symmetric=true);
|
||||
echo(__s2);
|
||||
for(t=[0:0.01:len(__s2)]) translate(spline(__s2, t))
|
||||
cube([0.2,0.2,0.2], center=true);
|
||||
|
||||
// Rotation methods taken from list-comprehension-demos/sweep.scad to demonstrate normal and binormal
|
||||
// Normally spline_transform is more convenient
|
||||
function __rotation_from_axis(x,y,z) = [[x[0],y[0],z[0]],[x[1],y[1],z[1]],[x[2],y[2],z[2]]];
|
||||
function __rotate_from_to(a,b,_axis=[]) =
|
||||
len(_axis) == 0
|
||||
? __rotate_from_to(a,b,unit(cross(a,b)))
|
||||
: _axis*_axis >= 0.99 ? __rotation_from_axis(unit(b),_axis,cross(_axis,unit(b))) *
|
||||
transpose_3(__rotation_from_axis(unit(a),_axis,cross(_axis,unit(a)))) : identity3();
|
||||
|
||||
__s3 = spline_args([[0,10,0], [6,6,0], [10,0,0],[0,-5,4]], v1=[0,1,0], v2=[-1,0,0], closed=true);
|
||||
for(t=[0:0.05:len(__s3)]) translate(spline(__s3, t)) {
|
||||
translate([0,0,3]) multmatrix(m=__rotate_from_to([0,0,1],spline_normal_unit(__s3,t)))
|
||||
cylinder(r1=0.1, r2=0, h=1, $fn=3);
|
||||
translate([0,0,6]) multmatrix(m=__rotate_from_to([0,0,1],spline_binormal_unit(__s3,t)))
|
||||
cylinder(r1=0.1, r2=0, h=1, $fn=3);
|
||||
}
|
||||
|
||||
translate([0,0,9]) for(t=[0:0.025:len(__s3)])
|
||||
multmatrix(spline_transform(__s3,t)) cube([1,1,0.1],center=true);
|
||||
|
||||
|
||||
|
||||
43
src/libraries/scad-utils/trajectory.scad
Normal file
43
src/libraries/scad-utils/trajectory.scad
Normal file
|
|
@ -0,0 +1,43 @@
|
|||
use <so3.scad>
|
||||
|
||||
function val(a=undef,default=undef) = a == undef ? default : a;
|
||||
function vec_is_undef(x,index_=0) = index_ >= len(x) ? true :
|
||||
is_undef(x[index_]) && vec_is_undef(x,index_+1);
|
||||
|
||||
function is_undef(x) = len(x) > 0 ? vec_is_undef(x) : x == undef;
|
||||
// Either a or b, but not both
|
||||
function either(a,b,default=undef) = is_undef(a) ? (is_undef(b) ? default : b) : is_undef(b) ? a : undef;
|
||||
|
||||
function translationv(left=undef,right=undef,up=undef,down=undef,forward=undef,backward=undef,translation=undef) =
|
||||
translationv_2(
|
||||
x = either(up,-down),
|
||||
y = either(right,-left),
|
||||
z = either(forward,-backward),
|
||||
translation = translation);
|
||||
|
||||
function translationv_2(x,y,z,translation) =
|
||||
x == undef && y == undef && z == undef ? translation :
|
||||
is_undef(translation) ? [val(x,0),val(y,0),val(z,0)]
|
||||
: undef;
|
||||
|
||||
function rotationv(pitch=undef,yaw=undef,roll=undef,rotation=undef) =
|
||||
rotation == undef ? [val(yaw,0),val(pitch,0),val(roll,0)] :
|
||||
pitch == undef && yaw == undef && roll == undef ? rotation :
|
||||
undef;
|
||||
|
||||
function trajectory(
|
||||
left=undef, right=undef,
|
||||
up=undef, down=undef,
|
||||
forward=undef, backward=undef,
|
||||
translation=undef,
|
||||
|
||||
pitch=undef,
|
||||
yaw=undef,
|
||||
roll=undef,
|
||||
rotation=undef
|
||||
) = concat(
|
||||
translationv(left=left,right=right,up=up,down=down,forward=forward,backward=backward,translation=translation),
|
||||
rotationv(pitch=pitch,yaw=yaw,roll=roll,rotation=rotation)
|
||||
);
|
||||
|
||||
function rotationm(rotation=undef,pitch=undef,yaw=undef,roll=undef) = so3_exp(rotationv(rotation=rotation,pitch=pitch,yaw=yaw,roll=roll));
|
||||
89
src/libraries/scad-utils/trajectory_path.scad
Normal file
89
src/libraries/scad-utils/trajectory_path.scad
Normal file
|
|
@ -0,0 +1,89 @@
|
|||
use <linalg.scad>
|
||||
use <se3.scad>
|
||||
|
||||
function left_multiply(a,bs,i_=0) = i_ >= len(bs) ? [] :
|
||||
concat([
|
||||
a * bs[i_]
|
||||
], left_multiply(a,bs,i_+1));
|
||||
|
||||
|
||||
function right_multiply(as,b,i_=0) = i_ >= len(as) ? [] :
|
||||
concat([
|
||||
as[i_] * b
|
||||
], right_multiply(as,b,i_+1));
|
||||
|
||||
function quantize_trajectory(trajectory,step=undef,start_position=0,steps=undef,i_=0,length_=undef) =
|
||||
length_ == undef ? quantize_trajectory(
|
||||
trajectory=trajectory,
|
||||
start_position=(step==undef?norm(take3(trajectory))/steps*start_position:start_position),
|
||||
length_=norm(take3(trajectory)),
|
||||
step=step,steps=steps,i_=i_) :
|
||||
(steps==undef?start_position > length_:i_>=steps) ? [] :
|
||||
concat([
|
||||
// if steps is defined, ignore start_position
|
||||
se3_exp(trajectory*(steps==undef ? start_position/length_
|
||||
: i_/(steps>1?steps-1:1)))
|
||||
], quantize_trajectory(trajectory=trajectory,step=step,start_position=(steps==undef?start_position+step:start_position),steps=steps,i_=i_+1,length_=length_));
|
||||
|
||||
function close_trajectory_loop(trajectories) = concat(trajectories,[se3_ln(invert_rt(trajectories_end_position(trajectories)))]);
|
||||
|
||||
function quantize_trajectories(trajectories,step=undef,start_position=0,steps=undef,loop=false,last_=identity4(),i_=0,current_length_=undef,j_=0) =
|
||||
// due to quantization differences, the last step may be missed. In that case, add it:
|
||||
loop==true ? quantize_trajectories(
|
||||
trajectories=close_trajectory_loop(trajectories),
|
||||
step=step,
|
||||
start_position = start_position,
|
||||
steps=steps,
|
||||
loop=false,
|
||||
last_=last_,
|
||||
i_=i_,
|
||||
current_length_=current_length_,
|
||||
j_=j_) :
|
||||
i_ >= len(trajectories) ? (j_ < steps ? [last_] : []) :
|
||||
current_length_ == undef ?
|
||||
quantize_trajectories(
|
||||
trajectories=trajectories,
|
||||
step = (step == undef ? trajectories_length(trajectories) / steps : step),
|
||||
start_position = (step == undef ? start_position * trajectories_length(trajectories) / steps : start_position),
|
||||
steps=steps,
|
||||
loop=loop,
|
||||
last_=last_,
|
||||
i_=i_,
|
||||
current_length_=norm(take3(trajectories[i_])),
|
||||
j_=j_) :
|
||||
concat(
|
||||
left_multiply(last_,quantize_trajectory(
|
||||
trajectory=trajectories[i_],
|
||||
start_position=start_position,
|
||||
step=step)),
|
||||
quantize_trajectories(
|
||||
trajectories=trajectories,
|
||||
step=step,
|
||||
start_position = start_position > current_length_
|
||||
? start_position - current_length_
|
||||
: step - ((current_length_-start_position) % step),
|
||||
steps=steps,
|
||||
loop=loop,
|
||||
last_=last_ * se3_exp(trajectories[i_]),
|
||||
i_=i_+1,
|
||||
current_length_ = undef,
|
||||
j_=j_+len(
|
||||
|
||||
quantize_trajectory(
|
||||
trajectory=trajectories[i_],
|
||||
start_position=start_position,
|
||||
step=step
|
||||
|
||||
))
|
||||
))
|
||||
;
|
||||
|
||||
|
||||
function trajectories_length(trajectories, i_=0) = i_ >= len(trajectories) ? 0
|
||||
: norm(take3(trajectories[i_])) + trajectories_length(trajectories,i_+1);
|
||||
|
||||
|
||||
function trajectories_end_position(rt,i_=0,last_=identity4()) =
|
||||
i_ >= len(rt) ? last_ :
|
||||
trajectories_end_position(rt, i_+1, last_ * se3_exp(rt[i_]));
|
||||
|
||||
43
src/libraries/scad-utils/transformations.scad
Normal file
43
src/libraries/scad-utils/transformations.scad
Normal file
|
|
@ -0,0 +1,43 @@
|
|||
use <se3.scad>
|
||||
use <linalg.scad>
|
||||
use <lists.scad>
|
||||
|
||||
/*!
|
||||
Creates a rotation matrix
|
||||
|
||||
xyz = euler angles = rz * ry * rx
|
||||
axis = rotation_axis * rotation_angle
|
||||
*/
|
||||
function rotation(xyz=undef, axis=undef) =
|
||||
xyz != undef && axis != undef ? undef :
|
||||
xyz == undef ? se3_exp([0,0,0,axis[0],axis[1],axis[2]]) :
|
||||
len(xyz) == undef ? rotation(axis=[0,0,xyz]) :
|
||||
(len(xyz) >= 3 ? rotation(axis=[0,0,xyz[2]]) : identity4()) *
|
||||
(len(xyz) >= 2 ? rotation(axis=[0,xyz[1],0]) : identity4()) *
|
||||
(len(xyz) >= 1 ? rotation(axis=[xyz[0],0,0]) : identity4());
|
||||
|
||||
/*!
|
||||
Creates a scaling matrix
|
||||
*/
|
||||
function scaling(v) = [
|
||||
[v[0],0,0,0],
|
||||
[0,v[1],0,0],
|
||||
[0,0,v[2],0],
|
||||
[0,0,0,1],
|
||||
];
|
||||
|
||||
/*!
|
||||
Creates a translation matrix
|
||||
*/
|
||||
function translation(v) = [
|
||||
[1,0,0,v[0]],
|
||||
[0,1,0,v[1]],
|
||||
[0,0,1,v[2]],
|
||||
[0,0,0,1],
|
||||
];
|
||||
|
||||
// Convert between cartesian and homogenous coordinates
|
||||
function project(x) = subarray(x,end=len(x)-1) / x[len(x)-1];
|
||||
|
||||
function transform(m, list) = [for (p=list) project(m * vec4(p))];
|
||||
function to_3d(list) = [ for(v = list) vec3(v) ];
|
||||
137
src/libraries/skin.scad
Normal file
137
src/libraries/skin.scad
Normal file
|
|
@ -0,0 +1,137 @@
|
|||
use <scad-utils/transformations.scad>
|
||||
use <scad-utils/lists.scad>
|
||||
|
||||
// Skin a set of profiles with a polyhedral mesh
|
||||
module skin(profiles, loop=false /* unimplemented */) {
|
||||
P = max_len(profiles);
|
||||
N = len(profiles);
|
||||
|
||||
profiles = [
|
||||
for (p = profiles)
|
||||
for (pp = augment_profile(to_3d(p),P))
|
||||
pp
|
||||
];
|
||||
|
||||
function quad(i,P,o) = [[o+i, o+i+P, o+i%P+P+1], [o+i, o+i%P+P+1, o+i%P+1]];
|
||||
|
||||
function profile_triangles(tindex) = [
|
||||
for (index = [0:P-1])
|
||||
let (qs = quad(index+1, P, P*(tindex-1)-1))
|
||||
for (q = qs) q
|
||||
];
|
||||
|
||||
triangles = [
|
||||
for(index = [1:N-1])
|
||||
for(t = profile_triangles(index))
|
||||
t
|
||||
];
|
||||
|
||||
start_cap = [range([0:P-1])];
|
||||
end_cap = [range([P*N-1 : -1 : P*(N-1)])];
|
||||
|
||||
polyhedron(convexity=2, points=profiles, faces=concat(start_cap, triangles, end_cap));
|
||||
}
|
||||
|
||||
// Augments the profile with steiner points making the total number of vertices n
|
||||
function augment_profile(profile, n) =
|
||||
subdivide(profile,insert_extra_vertices_0([profile_lengths(profile),dup(0,len(profile))],n-len(profile))[1]);
|
||||
|
||||
function subdivide(profile,subdivisions) = let (N=len(profile)) [
|
||||
for (i = [0:N-1])
|
||||
let(n = len(subdivisions)>0 ? subdivisions[i] : subdivisions)
|
||||
for (p = interpolate(profile[i],profile[(i+1)%N],n+1))
|
||||
p
|
||||
];
|
||||
|
||||
function interpolate(a,b,subdivisions) = [
|
||||
for (index = [0:subdivisions-1])
|
||||
let(t = index/subdivisions)
|
||||
a*(1-t)+b*t
|
||||
];
|
||||
|
||||
function distribute_extra_vertex(lengths_count,ma_=-1) = ma_<0 ? distribute_extra_vertex(lengths_count, max_element(lengths_count[0])) :
|
||||
concat([set(lengths_count[0],ma_,lengths_count[0][ma_] * (lengths_count[1][ma_]+1) / (lengths_count[1][ma_]+2))], [increment(lengths_count[1],max_element(lengths_count[0]),1)]);
|
||||
|
||||
function insert_extra_vertices_0(lengths_count,n_extra) = n_extra <= 0 ? lengths_count :
|
||||
insert_extra_vertices_0(distribute_extra_vertex(lengths_count),n_extra-1);
|
||||
|
||||
// Find the index of the maximum element of arr
|
||||
function max_element(arr,ma_,ma_i_=-1,i_=0) = i_ >= len(arr) ? ma_i_ :
|
||||
i_ == 0 || arr[i_] > ma_ ? max_element(arr,arr[i_],i_,i_+1) : max_element(arr,ma_,ma_i_,i_+1);
|
||||
|
||||
function max_len(arr) = max([for (i=arr) len(i)]);
|
||||
|
||||
function increment(arr,i,x=1) = set(arr,i,arr[i]+x);
|
||||
|
||||
function profile_lengths(profile) = [
|
||||
for (i = [0:len(profile)-1])
|
||||
profile_segment_length(profile,i)
|
||||
];
|
||||
|
||||
function profile_segment_length(profile,i) = norm(profile[(i+1)%len(profile)] - profile[i]);
|
||||
|
||||
// Generates an array with n copies of value (default 0)
|
||||
function dup(value=0,n) = [for (i = [1:n]) value];
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
use <scad-utils/transformations.scad>
|
||||
use <scad-utils/trajectory_path.scad>
|
||||
use <scad-utils/trajectory.scad>
|
||||
use <scad-utils/shapes.scad>
|
||||
|
||||
module fakeISOEnter(thickness_difference = 0){
|
||||
// 1u is the space taken upy by a 1u keycap.
|
||||
// unit is the space taken up by a unit space for a keycap.
|
||||
// formula is 1u + unit *(length - 1)
|
||||
|
||||
// t is all modifications to the polygon array
|
||||
t = thickness_difference/2 - (19.02 - 18.16);
|
||||
|
||||
function unit(length) = 19.02 * length;
|
||||
|
||||
pointArray = [
|
||||
[19.05 * (-.5) + t, 19.05 * (-1) + t],
|
||||
[19.05 * (0.5) - t, 19.05 * (-1) + t],
|
||||
[19.05 * (0.5) - t, 19.05 * (1) - t],
|
||||
[19.05 * (-0.75) + t, 19.05 * (1) - t],
|
||||
[19.05 * (-0.75) + t, 19.05 * (0) + t],
|
||||
[19.05 * (-0.5) + t, 19.05 * (0) + t]
|
||||
];
|
||||
|
||||
|
||||
/*translate([unit(-.5), unit(-1) + 0.86]){*/
|
||||
minkowski() {
|
||||
circle($corner_radius, $fn=20);
|
||||
offset(r=-$corner_radius * 2, $fn=20) polygon(points=pointArray);
|
||||
}
|
||||
/*}*/
|
||||
}
|
||||
|
||||
function isoEnter() = [
|
||||
[19.05 * (-.5) + (19.02 - 18.16), 19.05 * (-1) + (19.02 - 18.16)],
|
||||
[19.05 * (0.5) - (19.02 - 18.16), 19.05 * (-1) + (19.02 - 18.16)],
|
||||
[19.05 * (0.5) - (19.02 - 18.16), 19.05 * (1) - (19.02 - 18.16)],
|
||||
[19.05 * (-0.75) + (19.02 - 18.16), 19.05 * (1) - (19.02 - 18.16)],
|
||||
[19.05 * (-0.75) + (19.02 - 18.16), 19.05 * (0) + (19.02 - 18.16)],
|
||||
[19.05 * (-0.5) + (19.02 - 18.16), 19.05 * (0) + (19.02 - 18.16)]
|
||||
];
|
||||
|
||||
|
||||
path_definition = [
|
||||
trajectory(forward = 10, roll = 0),
|
||||
];
|
||||
|
||||
// sweep
|
||||
path = quantize_trajectories(path_definition, steps=100);
|
||||
|
||||
// skin
|
||||
myLen = len(path)-1;
|
||||
trans = [ for (i=[0:len(path)-1]) transform(path[i], isoEnter()) ];
|
||||
|
||||
translate([0,10,0])
|
||||
skin(trans);
|
||||
80
src/settings.scad
Normal file
80
src/settings.scad
Normal file
|
|
@ -0,0 +1,80 @@
|
|||
// keytop thickness, aka how many millimeters between the inside and outside of the top surface of the key
|
||||
$keytop_thickness = 1;
|
||||
// wall thickness, aka the thickness of the sides of the keycap. note this is the total thickness, aka 3 = 1.5mm walls
|
||||
$wall_thickness = 3;
|
||||
//whether stabilizer connectors are enabled
|
||||
$stabilizers = false;
|
||||
// font used for text
|
||||
$font="DejaVu Sans Mono:style=Book";
|
||||
// font size used for text
|
||||
$font_size = 6;
|
||||
// whether or not to render fake keyswitches to check clearances
|
||||
$clearance_check = false;
|
||||
|
||||
/* [Key profile] */
|
||||
|
||||
// width of the very bottom of the key
|
||||
$bottom_key_width = 18.16;
|
||||
// height (from the front) of the very bottom of the ke
|
||||
$bottom_key_height = 18.16;
|
||||
// how much less width there is on the top. eg top_key_width = bottom_key_width - width_difference
|
||||
$width_difference = 6;
|
||||
// how much less height there is on the top
|
||||
$height_difference = 4;
|
||||
// how deep the key is, before adding a dish
|
||||
$total_depth = 11.5;
|
||||
// the tilt of the dish in degrees. divided by key height
|
||||
$top_tilt = -6;
|
||||
// how skewed towards the back the top is (0 for center)
|
||||
$top_skew = 1.7;
|
||||
// what type of dish the key has. 0 for cylindrical, 1 for spherical, 2 for something else idk TODO
|
||||
$dish_type = "cylindrical";
|
||||
// how deep the dish 'digs' into the top of the keycap. this is max depth, so you can't find the height from total_depth - dish_depth. besides the top is skewed anyways
|
||||
$dish_depth = 1;
|
||||
// how skewed in the x direction the dish is
|
||||
$dish_skew_x = 0;
|
||||
// how skewed in the y direction (height) the dish is
|
||||
$dish_skew_y = 0;
|
||||
//length in units of key
|
||||
$key_length = 1;
|
||||
//height in units of key. should remain 1 for most uses
|
||||
$key_height = 1;
|
||||
//print brim for connector to help with bed adhesion
|
||||
$has_brim = false;
|
||||
// invert dishing. mostly for spacebar
|
||||
$inverted_dish = false;
|
||||
// array of positions of all stems. includes stabilizers as well, for now
|
||||
// ternary is a bad hack to keep the stabilizers flag working
|
||||
$connectors = $stabilizers ? [[0,0],[-50,0],[50,0]] : [[0,0]];
|
||||
// use linear_extrude instead of hull slices to make the shape of the key
|
||||
// should be faster, also required for concave shapes
|
||||
$linear_extrude_shape = false;
|
||||
//should the key be rounded? unnecessary for most printers, and very slow
|
||||
$rounded_key = false;
|
||||
// 'cherry', 'alps' or 'cherry_rounded'
|
||||
$stem_profile = "cherry";
|
||||
// how much higher the stem is than the bottom of the keycap.
|
||||
// inset stem requires support but is more accurate in some profiles
|
||||
$stem_inset = 0;
|
||||
// how many degrees to rotate the stems. useful for sideways keycaps, maybe
|
||||
$stem_rotation = 0;
|
||||
//text to be rendered in the center of the key, if any
|
||||
$text = "";
|
||||
// is the text on the key inset? inset text is still experimental
|
||||
$inset_text = false;
|
||||
// radius of corners of keycap
|
||||
$corner_radius = 1;
|
||||
// keystem slop - lengthens the cross and thins out the connector
|
||||
$slop = 0.3;
|
||||
// support type. default is 'flared' for easy FDM printing
|
||||
$support_type = "flared";
|
||||
// key shape type. default is 'normal'. only other supported option is 'iso_enter'
|
||||
$key_shape_type = "normal";
|
||||
// ISO enter needs to be linear extruded NOT from the center. this tells the program how far up 'not from the center' is
|
||||
$linear_extrude_height_adjustment = 0;
|
||||
// if you need the dish to extend further, you can 'overdraw' the rectangle it will hit
|
||||
$dish_overdraw_width = 0;
|
||||
// same as width but for height
|
||||
$dish_overdraw_height = 0;
|
||||
// how many slices will be made, to approximate curves on corners. Leave at 1 if you are not curving corners
|
||||
$height_slices = 1;
|
||||
60
src/shapes.scad
Normal file
60
src/shapes.scad
Normal file
|
|
@ -0,0 +1,60 @@
|
|||
$fs=.1;
|
||||
unit = 19.05;
|
||||
|
||||
module key_shape(width, height, width_difference, height_difference, corner_size) {
|
||||
if ($key_shape_type == "iso_enter") {
|
||||
ISO_enter(width, height, width_difference, height_difference, corner_size);
|
||||
} else if ($key_shape_type == "normal") {
|
||||
roundedSquare([width - width_difference, height - height_difference], corner_size);
|
||||
} else if ($key_shape_type == "circle") {
|
||||
circle(d=width - width_difference);
|
||||
}
|
||||
}
|
||||
|
||||
// centered
|
||||
module roundedRect(size, radius, center=true) {
|
||||
linear_extrude(height = size[2]){
|
||||
roundedSquare([size[0], size[1]], radius, center=center);
|
||||
}
|
||||
}
|
||||
|
||||
module roundedSquare(size, radius, center = true) {
|
||||
offset(r=radius){
|
||||
square([size[0] - radius * 2, size[1] - radius * 2], center=center);
|
||||
}
|
||||
}
|
||||
|
||||
// corollary is roundedSquare
|
||||
// NOT 3D
|
||||
module ISO_enter(width, height, width_difference, height_difference, corner_size){
|
||||
function unit_length(length) = unit * (length - 1) + 18.16;
|
||||
|
||||
|
||||
// in order to make the ISO keycap shape generic, we are going to express the
|
||||
// 'elbow point' in terms of ratios. an ISO enter is just a 1.5u key stuck on
|
||||
// top of a 1.25u key, but since our key_shape function doesnt understand that
|
||||
// and wants to pass just width and height, we make these ratios to know where
|
||||
// to put the elbow joint
|
||||
|
||||
width_ratio = unit_length(1.25) / unit_length(1.5);
|
||||
height_ratio = unit_length(1) / unit_length(2);
|
||||
|
||||
// height and width difference currently don't do anything - but I think I should keep them. they don't do anything because we currently use scaling in the linear_extrude to express the difference in height and width of the top of the keycap
|
||||
|
||||
pointArray = [
|
||||
[ -width_difference/2, -height_difference/2], // top right
|
||||
[ -width_difference/2, -height + height_difference/2], // bottom right
|
||||
[-width * width_ratio + width_difference/2, -height + height_difference/2], // bottom left
|
||||
[-width * width_ratio + width_difference/2,-height * height_ratio + height_difference/2], // inner middle point
|
||||
[ -width + width_difference/2,-height * height_ratio + height_difference/2], // outer middle point
|
||||
[ -width + width_difference/2, -height_difference/2] // top left
|
||||
];
|
||||
|
||||
minkowski(){
|
||||
circle(r=corner_size);
|
||||
// gives us rounded inner corner
|
||||
offset(r=-corner_size*2) {
|
||||
translate([(width * width_ratio)/2, height/2]) polygon(points=pointArray);
|
||||
}
|
||||
}
|
||||
}
|
||||
146
src/stems.scad
Normal file
146
src/stems.scad
Normal file
|
|
@ -0,0 +1,146 @@
|
|||
include <supports.scad>
|
||||
|
||||
brim_height = 0.4;
|
||||
|
||||
//whole connector, alps or cherry, trimmed to fit
|
||||
module connector(stem_profile, depth, has_brim, slop, stem_inset, support_type){
|
||||
echo(slop);
|
||||
if (stem_profile == "alps") {
|
||||
alps_stem(depth, has_brim, slop, stem_inset, support_type);
|
||||
} else if (stem_profile == "cherry_rounded") {
|
||||
cherry_stem_rounded(depth, has_brim, slop, stem_inset, support_type);
|
||||
} else if (stem_profile == "cherry") {
|
||||
cherry_stem(depth, has_brim, slop, stem_inset, support_type);
|
||||
} else if (stem_profile == "filled") {
|
||||
// just a cube, so no args
|
||||
filled_stem();
|
||||
}
|
||||
}
|
||||
|
||||
module cherry_stem(depth, has_brim, slop, stem_inset, support_type) {
|
||||
stem_width = 7.2 - slop * 2;
|
||||
stem_height = 5.5 - slop * 2;
|
||||
|
||||
vertical_cross_width = 1.25;
|
||||
// currently unused, as we want a split stem
|
||||
vertical_cross_length = 3.93;
|
||||
|
||||
horizontal_cross_width = 1.15;
|
||||
horizontal_cross_length = 4.03;
|
||||
|
||||
cross_depth = 4;
|
||||
|
||||
stem = [stem_width, stem_height];
|
||||
vertical_cross = [vertical_cross_width, stem_height];
|
||||
horizontal_cross = [horizontal_cross_length + slop, horizontal_cross_width];
|
||||
|
||||
translate([0,0,stem_inset]) {
|
||||
difference(){
|
||||
union() {
|
||||
linear_extrude(height = depth) {
|
||||
roundedSquare(stem, 1, center=true);
|
||||
}
|
||||
if(has_brim) {
|
||||
roundedRect([stem_width*2, stem_height*2,brim_height], 1, 1, center=true);
|
||||
}
|
||||
}
|
||||
linear_extrude(height = cross_depth) {
|
||||
square(vertical_cross, center=true);
|
||||
square(horizontal_cross, center=true);
|
||||
}
|
||||
}
|
||||
|
||||
// supports
|
||||
if (support_type == "flared") {
|
||||
flared(cross_depth, (depth - cross_depth), [stem_width, stem_height]) {
|
||||
roundedSquare(stem, 1, center=true);
|
||||
}
|
||||
} else if (support_type == "flat") {
|
||||
flat(cross_depth, (depth - cross_depth), [stem_width, stem_height]);
|
||||
} else if (support_type == "bars") {
|
||||
bars(cross_depth, (depth - cross_depth), [stem_width, stem_height]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module cherry_stem_rounded(depth, has_brim, slop, stem_inset, support_type) {
|
||||
// cross length
|
||||
cross_length = 4.4;
|
||||
//dimensions of connector
|
||||
// outer cross extra length in y
|
||||
extra_outer_cross_height = 1.1;
|
||||
// dimensions of cross
|
||||
// horizontal cross bar width
|
||||
horizontal_cross_width = 1.4;
|
||||
// vertical cross bar width
|
||||
vertical_cross_width = 1.3;
|
||||
// cross depth, stem height is 3.4mm
|
||||
cross_depth = 4;
|
||||
|
||||
total_diameter = cross_length+extra_outer_cross_height;
|
||||
|
||||
translate([0,0,stem_inset]){
|
||||
difference(){
|
||||
union(){
|
||||
cylinder(d=total_diameter, h=depth);
|
||||
if(has_brim) {
|
||||
cylinder(d=total_diameter * 2, h=brim_height);
|
||||
}
|
||||
}
|
||||
//the cross part of the steam
|
||||
translate([0,0,(cross_depth)/2]){
|
||||
cube([vertical_cross_width,cross_length,cross_depth], center=true );
|
||||
cube([cross_length,horizontal_cross_width,cross_depth], center=true );
|
||||
}
|
||||
}
|
||||
|
||||
// supports
|
||||
if (support_type == "flared") {
|
||||
flared(cross_depth, (depth - cross_depth)) {
|
||||
circle(d = cross_length+extra_outer_cross_height);
|
||||
}
|
||||
} else if (support_type == "flat") {
|
||||
flat(cross_depth, (depth - cross_depth));
|
||||
} else if (support_type == "bars") {
|
||||
bars(cross_depth, (depth - cross_depth));
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module alps_stem(depth, has_brim, slop, stem_inset, support_type){
|
||||
// not really cross depth, basically just the max length of stem we need for the key to function properly
|
||||
cross_depth = 4;
|
||||
|
||||
width = 4.45;
|
||||
height = 2.25;
|
||||
|
||||
base_width = 12;
|
||||
base_height = 15;
|
||||
|
||||
translate([0,0,stem_inset]){
|
||||
if(has_brim) {
|
||||
translate([0,0,brim_height / 2]) cube([width*2,height*2,brim_height], center = true);
|
||||
}
|
||||
translate([0,0,depth/2]){
|
||||
cube([width,height,depth], center = true);
|
||||
}
|
||||
}
|
||||
|
||||
translate([0, 0, stem_inset]){
|
||||
if (support_type == "flared") {
|
||||
flared(cross_depth, (depth - cross_depth)) {
|
||||
square([width,height]);
|
||||
}
|
||||
} else if (support_type == "flat") {
|
||||
flat(cross_depth, (depth - cross_depth));
|
||||
} else if (support_type == "bars") {
|
||||
bars(cross_depth, (depth - cross_depth));
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module filled_stem() {
|
||||
// this is mostly for testing. we don't pass the size of the keycp in here
|
||||
// so we can't make this work for all keys
|
||||
cube(1000, center=true);
|
||||
}
|
||||
21
src/supports.scad
Normal file
21
src/supports.scad
Normal file
|
|
@ -0,0 +1,21 @@
|
|||
// flared support designed for FDM printing, for the normal cherry stem
|
||||
module flared(loft, height) {
|
||||
translate([0,0,loft]){
|
||||
linear_extrude(height=height, scale = [height/2,height/2]){
|
||||
children();
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
module flat(loft, height) {
|
||||
translate([0,0,loft + 500]){
|
||||
cube(1000, center=true);
|
||||
}
|
||||
}
|
||||
|
||||
module bars(loft, height) {
|
||||
translate([0,0,loft + height / 2]){
|
||||
cube([2, 100, height], center = true);
|
||||
cube([100, 2, height], center = true);
|
||||
}
|
||||
}
|
||||
Loading…
Add table
Add a link
Reference in a new issue